SOLUTION: Hi, My problem is: The value of a two-digit number is twice as large as the sum of its digits. If the digits were reversed, the resulting number would be 9 less than 5 times

Click here to see ALL problems on Miscellaneous Word Problems

Question 719734: Hi,
My problem is:

The value of a two-digit number is twice as large as the sum of its digits. If the digits were reversed, the resulting number would be 9 less than 5 times the number. Find the original number.
Please explain in detail.
Thanks
Found 2 solutions by josgarithmetic, solver91311:
Answer by josgarithmetic(39617) (Show Source):
You can put this solution on YOUR website!
X and Y are the digits. The number is 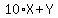, taking care of place value for this two digit number.

First condtion:

Second condition, a bit complicated, but .

You should simplify each of those equations, and then solve for X and Y.

First Condition: 10X+Y=2X+2Y,
..

Second Condition: 10Y+X-5(10X+Y)=-9
10Y+X-50X-5Y=-9
-49X+5Y=-9

SYSTEM TO SOLVE:

I tried solving both equations for y, equate them, and solve for the value of x... . Using that, 8*x-y=0, y=8*x, y=8*1, .
Number is 18.

Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!

Let represent the 10s digit of the desired number. Let represent the 1s digit of the desired number. Then the desired number can be represented by:

and the sum of the digits can be represented by

So if the number is twice as large as the sum of its digits:

Which simplifies to:

The new number when the digits reversed would be represented by:

Five times the original number, less 9:

Then

Which simplifies to

Since we know that , substitute for in and solve for . Then substitute the computed value of into to find the value of .

Actually, you could have stopped right after you had established that . There is only one pair of single-digit positive integers that satisfies this equation.

John

Egw to Beta kai to Sigma
My calculator said it, I believe it, that settles it