SOLUTION: I am having a difficult time solving a few problems: here is the first problem: ln(x-3)+ln(3x+1)=10 I am not sure where to start the process to solve this problem, any help or

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: I am having a difficult time solving a few problems: here is the first problem: ln(x-3)+ln(3x+1)=10 I am not sure where to start the process to solve this problem, any help or      Log On


   

Question 719670: I am having a difficult time solving a few problems:
here is the first problem: ln(x-3)+ln(3x+1)=10
I am not sure where to start the process to solve this problem, any help or guidance is greatly appreciated.
Found 2 solutions by swincher4391, jsmallt9:
Answer by swincher4391(1107) About Me  (Show Source):
You can put this solution on YOUR website!
The key to this problem is to understand the logarithmic properties. The property invoked in this problem is the multiplication property. That is ln(a) + ln(b) = ln(ab).
Using this we know that ln(x-3)+ln(3x+1) is really ln[(x-3)(3x+1)].
So ln[(x-3)(3x+1)] = 10.
By FOIL:
ln[3x^2 -8x -3] = 10
Since ln is the natural log [with base e], we can EXPONENTIATE both sides by a base of e.
e^ln[3x^2-8x-3] = e^10
3x^2 - 8x - 3 = e^10
3x^2 - 8x - 3-e^10 = 0

Use the quadratic formula to clean this up:
%288+%2B-+sqrt%2864+-+%284%2A3%2A%28-3-e%5E10%29%29%29%29%2F+6%29
Which is roughly:
x= 87.036, -84.369
Remember that domain of the natural log is (0, infinity). So -84.369 will give us a negative in the logarithm which is not allowed. So the only acceptable solution is 87.036 or in exact form: %288+%2B+sqrt%28100+%2B+12e%5E10%29%29%29%29%2F+6%29 which may be simplified to:
%288+%2B+sqrt%284%2A%2825%2B3e%5E10%29%29%29%2F6
%288+%2B+2%2Asqrt%2825%2B3e%5E10%29%29%2F6
%284+%2B+sqrt%2825%2B3e%5E10%29%29%2F3 <--- in simplest form

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
ln%28x-3%29%2Bln%283x%2B1%29=10
Solving equations where the variable is in the argument (or base) of a logarithm, like yours, usually starts by transforming the equation into one of the following general forms:
log(expression) = number
or
log(expression) = log(expression)

It will be more difficult to transform your equation, with its "non-log" term of 10, into the "all-log" second form. So we will aim for the first form. For the first form will will need to find a way to combine the two logs into one.

There are two ways to combine logarithmic terms:
  • Add (or subtract) them if they are like terms. (Like logarithmic terms have the same bases and the same arguments.)
  • Use one of the following properties of logarithms:
    • log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Aq%29%29
    • log%28a%2C+%28p%29%29+-+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Fq%29%29
    These properties require logs of the same base and coefficients of 1.
The two logs on the left side have the same bases, e. But their arguments, x-3 and 3x+1, are different so we cannot add them together. The logs do, however, have coefficients of 1. So we can use the properties. We will use the first property because its logs, like yours, have a "+" between them:
ln%28%28x-3%29%2A%283x%2B1%29%29=10
or
ln%283x%5E2-8x-3%29+=+10
We now have the first form.

The next step with the first form is to rewrite the equation in exponential form. In general log%28a%2C+%28p%29%29+=+n is equivalent to p+=+a%5En. Using this property on our equation we get:
3x%5E2-8x-3+=+e%5E10
This is a quadratic equation which we can now solve for x. With quadratics you want one side to be zero. Subtracting 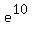e%5E10 we get:
3x%5E2-8x-3-e%5E10=0
Replacing 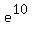e%5E10 with a decimal approximation:
3x%5E2-8x-3-22026.465794806716516957900645284=0
(Feel free to round off the decimal as you choose.) This simplifies to:
3x%5E2-8x-22029.465794806716516957900645284=0
Now we use the Quadratic Formula:

Simplifying...

x+=+%28-%28-8%29%2B-sqrt%2864%2B264353.58953768059820349480774341%29%29%2F2%283%29
x+=+%28-%28-8%29%2B-sqrt%28264417.58953768059820349480774341%29%29%2F2%283%29
x+=+%288+%2B-+sqrt%28264417.58953768059820349480774341%29%29%2F6
x+=+%288+%2B-+514.21550884593183203635910499516%29%2F6
which is short for:
x+=+%288+%2B+514.21550884593183203635910499516%29%2F6 or x+=+%288+-+514.21550884593183203635910499516%29%2F6
Simplifying...
x+=+%28522.21550884593183203635910499516%29%2F6 or x+=+%28-506.21550884593183203635910499516%29%2F6
x+=+87.035918140988638672726517499193 or x+=+%0D%0A-84.369251474321972006059850832526

Now we check. This is not optional when solving logarithmic equations like this. You must at least check to see that all arguments and bases of all logarithms remain valid when the variable is equal to the solution. (Valid arguments and bases are positive. Also, valid bases may not be 1.) If any argument or base of any logarithm turns out invalid, we must reject that "solution".

Use the original equation to check:
ln%28x-3%29%2Bln%283x%2B1%29=10
Checking x = 87.035918140988638672726517499193

We can already see that both bases are e's and both arguments will turn out to be positive numbers. So this solution checks out.

Checking x = -84.369251474321972006059850832526

We can already see that both bases are e's but both arguments will turn out negative. So this "solution" fails the check. We must reject it. If only one argument had been invalid we would have still rejected this solution.)

So there is only one solution to this equation:
approximately 87.035918140988638672726517499193