SOLUTION: I am having a real hard time solving this. I can't get the light bulb in my head to go ding when it comes to polynomials etc..Any help will be appreciated. 6 x ^ 2 - 2 3 x + 1 5

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I am having a real hard time solving this. I can't get the light bulb in my head to go ding when it comes to polynomials etc..Any help will be appreciated. 6 x ^ 2 - 2 3 x + 1 5      Log On


   

Question 71941: I am having a real hard time solving this. I can't get the light bulb in my head to go ding when it comes to polynomials etc..Any help will be appreciated.
6 x ^ 2 - 2 3 x + 1 5 = 0
Found 2 solutions by bucky, jim_thompson5910:
Answer by bucky(2189) About Me  (Show Source):
You can put this solution on YOUR website!
6x%5E2+-+23x+%2B+15+=+0
.
This can be solved in several ways. The easiest on ... once you see it is by factoring.
The left side of this equation factors to:
.
%28x-3%29%2A%286x+-+5%29+=+0
.
This equation will hold true if either of the factors equals zero. So we can find the answers
for x by first setting %28x-3%29+=+0. By adding 3 to both sides we get as one answer
to this problem x+=+3. Next set the second factor equal to zero to get 6x+-+5+=+0.
Solve by first adding 5 to both sides to get 6x+=+5. Then divide both sides by 6 and
you find the second value of x is x+=+5%2F6.
.
Another way to do this is to use the quadratic formula. This formula says that if you are
given a quadratic equation in the general form:
.
ax%5E2+%2B+bx+%2B+c+=+0
.
The values of x that satisfy this equation are:
.
x+=+-b%2F%282%2Aa%29+%2B-+sqrt%28b%5E2+-+%284%2Aa%2Ac%29%29%2F%282%2Aa%29
.
By comparing the general form to the problem you were given you can see that a = 6, b = -23,
and c = 15. Now just plug these values into the equation for x to get:
.
x+=+-%28-23%29%2F%282%2A6%29+%2B-+sqrt%2823%5E2+-+%284%2A6%2A15%29%29%2F%282%2A6%29
.
First simplifications lead to:
.
x+=+23%2F12+%2B-+sqrt%28529+-+%28360%29%29%2F12
.
And further:
.
x+=+23%2F12+%2B-+sqrt%28169%29%2F12
.
and sqrt(169) = 13 so the problem becomes:
.
x+=+23%2F12+%2B-+13%2F12
.
So the two answers are:
.
x+=+%2823%2B13%29%2F12=+36%2F12+=+3
.
and
.
x+=+%2823-13%29%2F12=+10%2F12+=+5%2F6
.
These answers are the same as we got by factoring. So they serve to verify that they are
correct.
.
I hope these couple of ways of doing the problem help you to see how you can solve
quadratic equations. Using the quadratic formula is the most general way. It always works.
But not all quadratic equations factor nicely.

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
When you're factoring polynomials you're taking a sum of terms (for example 6 x ^ 2 - 2 3 x + 1 5) and turning them into a product of factors (x+?)(x+?). If we have ax^2+bx+c we can turn that into (x+m)(x+n) where m and n are extra constants. This is just like factoring a real number into prime factors. For instance the number 56 can be factored into smaller factors
56=8%2A7
Which closely represents (x+m)(x+n), say we let x=5, m=3,n=2 then
it comes to (5+3)(5+2)=(8)(7).


This product can be written as a sum also. Say we knew m and n, but not x. We couldnt mix the x's and the numbers, but we can FOIL it.
56=%28x%2B3%29%28x%2B2%29
56=x%2Ax%2B2%2Ax%2B3%2Ax%2B6
56=x%5E2%2B5x%2B6Now we have a polynomial.


In this case we're going to work backwards: we're going from a sum (6x^2 - 23x + 15) to a product (cx+m)(dx+n) (where c and d are equal to 1 sometimes) which will FOIL to cdx^2+cnx+dmx+mn (or sometimes x^2+nx+mx+mn). The result cdx^2+cnx+dmx+mn is equal to 6x^2 - 23x + 15 and you can see the terms line up.

			6x^ 2         - 23 x        +       15
			cdx^2         +(cnx+dmx)    +       mn

The last term of 15 is equal to mn (ie mn=15), cdx^2=6x^2, and cnx+dmx=-23x. The trick is to find c,d,m, and n. The last term mn is equal to 15 so our factors could be 1,3,5,15 or -1,-3,-5,-15 (in other words: say m=3,n=5 mn=3*5=15. This is possible for any combination of factors that multiply to 15). To find c and d, notice how cdx^2=6x^2. If we get rid of the x^2 it comes to cd=6, so the factors of 6 are 1,2,3,6.


Also since the middle term is negative we know that cnx+dmx is negative. Since the last term is positive and the middle term is negative, m and n must both be negative. If I multiply two negative numbers, I get a positive number; If I add two negative numbers, I get a negative number. So lets try a few combinations of these factors: let c=1,d=6,m=-15,n=-1
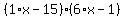
%281%2Ax-15%29%286%2Ax-1%29
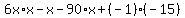
6x%2Ax-x-90%2Ax%2B%28-1%29%28-15%29
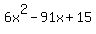6x%5E2-91x%2B15 We got 2 of the 3 terms of the polynomial, but instead of -91 we need -23 for the middle term. So lets try again, let c=1,d=6,m=-5,n=-3:
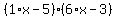
%281%2Ax-5%29%286%2Ax-3%29
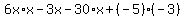
6x%2Ax-3x-30%2Ax%2B%28-5%29%28-3%29
6x%5E2-33x%2B15Again we got everything but the middle, so lets try another pair let c=1,d=6,m=-3,n=-5:
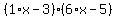
%281%2Ax-3%29%286%2Ax-5%29
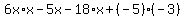
6x%2Ax-5x-18%2Ax%2B%28-5%29%28-3%29
6x%5E2-23x%2B15We finally got it (well I already knew the answer, if I didn't know it I would have to try more combinations). To find the right combo it takes a lot of practice and a bit of luck. In short, 6x^2-23x+15 factors to (x-3)(6x-5).


Now take this product and set it equal to zero.
%28x-3%29%286x-5%29=0This resembles ab=0 where a=(x-3) b=(6x-5). To solve for a, divide both sides by b (or 6x-5)
x-3=0Now we can find x
x=3There's one answer, do the same thing but find b
6x-5=0
6x=5
x=5%2F6There's our other answer. These 2 answers are the roots (x-intercepts) to the polynomial. If we plug in x=3 or x=5/6 into (x-3)(6x-5) or 6x^2-23x+15 we will get zero. I hope at least one sentence of this makes sense (I'm sure you got most of it) so feel free to ask even more questions after this explanation. If you want a quick way, graph it and find the x-intercepts.
graph%28+300%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+6x%5E2-23x%2B15%29 The solution represents the roots