Question 71840: create three unique equations where the discriminant is positive, zero, or negative using the quadratic formula to solve a quadratic equation ( ax^2 + bx + c=0) the discriminant is b^2-4ac
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the discriminant is positive you get two real answers to the quadratic.
We could do this by saying that we want  to be larger than to be larger than 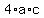 . .
So let's
say that  so that so that  . Now let's assume . Now let's assume 
and
therefore, as long as 4*c is less than 36 we will have a positive discriminant. So
let's say that  . Solving this we see that . Solving this we see that  . .
So we have a = 1, b = 6, and c = 5. This makes the quadratic equation:

.
and the discriminant is:
.

.
(Just for your info, if you solve  you will find that you will find that  or or
 are the answers. are the answers.
.
Now let's find a case where the discriminant equals zero. For this case, we need to
make  equal to equal to 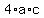 . Again, we will assume that a = 1 just to simplify . Again, we will assume that a = 1 just to simplify
things. This reduces the problem to making  equal to equal to 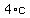 . .
.
Let's assign a value of 8 to b. This means that  . Therefore, we need to . Therefore, we need to
make 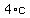 equal to 64. Solving this we find that equal to 64. Solving this we find that  . So our values for . So our values for
the quadratic equation are a = 1, b = 8, and c = 16. Plugging these into the standard
form of a quadratic equation we get:
.

.
If you calculate the discriminant you will find that it equals zero, just as we figured it
would. And the answer for x in this equation is x= 4.
.
To find an equation that has no real solution, all we need to do is make 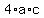
greater than  . Again, for simplification let a = 1. Then we just need to have . Again, for simplification let a = 1. Then we just need to have
 be less than be less than 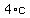 . Let's assume b = 2. Then . Let's assume b = 2. Then  . So all we . So all we
now need to do is make sure that 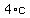 is greater than 4. So let's make c equal 3. is greater than 4. So let's make c equal 3.
Then  and this is greater than and this is greater than  . .
.
We have now found the following values: a = 1, b = 2, and c = 3. So the corresponding
quadratic equation is:
.

.
If you solve for the discriminant you will find that it has a negative value, and if
you further solve for x using the quadratic formula you will find that the two answers are:
.
 and and 
.
I hope this helps you to see your way through this problem. Check the math above. I
think it's correct, but it's pretty late at night to work error free.
|
|
|