Question 718316: Hello,
I am trying to graph an absolute value equation and cannot seem to solve it.
the equation is to Solve |2x+2|=-2/3x+2 Graphically.
In my answer booklet it says the 2 answer to this absolute value equation is x=-3 and x=0 but when I plot these two equations i notice that they both have a y intercept of 2 so, i thought that they would meet at x=2. Please help me, it would be greatly appreciated! Best of Luck.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! First of all, please put fractions which are factors in parentheses. The right side, as you posted it, means:
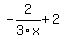
It was only your mention that the y-intercept was 2 that allowed me to figure out that it was supposed to be:
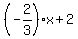
description that the
At the y-intercept of 2, the y-coordinate is 2. The x-coordinate on the y-axis is always 0. This explains the x=0 solution.
As for the other solution...
The graphs of equations of the form:
y = | mx+b |
will "bounce" off the x-axis. They will "bounce" at the point whose x-coordinate is the number that makes mx+b be zero. For y = | 2x+2 |, the graph will "bounce" off the x-axis at -1 because -1 makes 2x+2 be zero. (If you can't see this, just set 2x+2 = 0 and solve for x.)
The graph of y = | mx + b | will be the graphs of two "half-lines" which meet at the "bounce" point. One "half-line" will the part of the graph of y = mx+b that is above the x-axis and the other "half-line" will the the part of the graph of y = -(mx+b) (or y - -mx-b) which is above the x-axis.
For y = | 2x+2 |, the two "half-lines" would be: y = 2x+2 and y = -2x-2. The first "half-line" is the one whose y-intercept is 2 and intersects  there. The other "half-line", y = -2x-2, will intersect somewhere to the left of the "bounce" point at (-1, 0).
Here's a graph of both y = | 2x+2 | and :
|
|
|
