SOLUTION: Find the domain and range of the graph of each function. y=log2(x-3) (2 is the base of the log) WE were told that the answer would involve inf. -inf or xero

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Find the domain and range of the graph of each function. y=log2(x-3) (2 is the base of the log) WE were told that the answer would involve inf. -inf or xero      Log On


   

Question 71811: Find the domain and range of the graph of each function. y=log2(x-3)
(2 is the base of the log) WE were told that the answer would involve inf. -inf or xero
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
Find the domain and range of the graph of each function. y=log2(x-3)
(2 is the base of the log)
-------------------
y=log2(x) has domain (0,inf) and range (-inf,inf)
But you have y=log2(x-3):
The x-3 moves the x values 3 to the right and leaves the y values as they were.
So, domain is (3,inf) and range is (-inf,inf).
=========
Cheers,
Stan H.

Answer by Edwin McCravy(20063) About Me  (Show Source):
You can put this solution on YOUR website!
Find the domain and range of the graph of each function. 
y=log2(x-3). WE were told that the answer would involve 
inf. -inf or zero

Only logarithms of positive numbers are defined.   Therefore log2(x-3) 
is only defined when x-3 is positive, or

                          x - 3 > 0
                              x > 3

So the domain is (3, ¥)

Plot the graph by y = log2(x-3) getting some points, say

(4,0), (5,1), (7,2), (11,3) (3.25, -2)

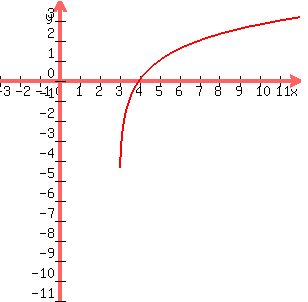+graph%28300%2C+300%2C+-3%2C+12%2C+-11%2C+4%2C+ln%28x-3%29%2Fln%282%29%29  

The vertical line (drawn in green below) has equation x = 3 
and it is an asymptote:

+graph%28300%2C+300%2C+-3%2C+12%2C+-11%2C+4%2C+ln%28x-3%29%2Fln%282%29%2C+999%28x-3%29%29

So the range (the set of possible y-values) contains all real 
values and is thus (-¥, ¥)

Edwin