|
Question 717911: Homework! I got lost on this question it would be a HUGE help if someone can answer this ASAP
x3+4x2 / x2-1 Multiply x2-5x+6 / x2-3x DIVIDE x2+2x-8 / x2-1
Simplify and state all restrictions
The dashes are division the numerator and denominator
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
The last thing we want to do is to start multiplying. We would be making this an extremely difficult problem by doing so. We will start by factoring. We do this for two reasons. With the numerators and denominators of this original expression in factored form...- We will be able to determine the restrictions on the values for x.
- We will be able to cancel some of these factors, making the expression simpler, before we multiply.
Every numerator and denominator factors:
We will come back to this when we do the restrictions. But now I want to start simplifying. First we'll turn the division by 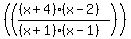 into multiplication by its reciprocal:
Now we start canceling factors that are common to the numerator and denominator. And since this is all multiplication of fractions, we are allowed to croos-cancel (cancel a factor in one fraction's numerator with a factor in another fraction's denominator and vice versa).
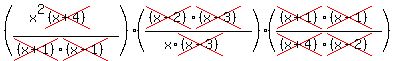
If we write  as x*x we can cancel a little more:
This leaves just x! By simplifying first, we didn't have to multiply anything! So  ... with restrictions.
To determine the restrictions on x, let's go back to the factored form of the original expression:
The restrictions are that we cannot allow x to have a value that would make a denominator become zero. We have 4 denominators, 3 denominators of what I call the "little" fractions and 1 denominator of what I call the "big" fraction. Let's deal with that last one first. The denominator of the "big" fraction is:
This denominator is itself a fraction. A fraction is zero only if its numerator is zero. So if we set the numerator equal to zero and solve, we will find some values which must not be allowed to have because they make this "big" fraction's denominator zero:
(x+4)(x-2) = 0
From the Zero Product Property:
x+4 = 0 or x-2 = 0
Solving these we get:
x = -4 or x = 2
Now we'll start on the denominators of the "little" fractions. First:
(x+1)(x-1) = 0
x+1 = 0 or x-1 = 0
x = -1 or x = 1
Next:
x(x-3) = 0
x = 0 or x-3 = 0
x = 0 or x = 3
Last:
(x+1)(x-1)
This is the same as the first "little" denominator so its solution will be the same.
So altogether is x is -4, -1, 0, 1, 2 or 3 at least one denominator will be zero. So in conclusion:
where x is any real number except -4, -1, 0, 1, 2 or 3
|
|
|
| |
