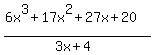
Start with this:
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
3x divides into 6x³ to give 2x²
Put that at the top, above the 17x²
2x²
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
Multiply the 2x² by the 3x + 4 to get 6x³ + 8x²,
so write that at the bottom and draw a line:
2x²
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
Now subtract, by mentally changing the signs on
the bottom row. We get 9x², so we write that
at the bottom, and bring down the next term 27x:
2x²
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
3x divides into 9x² to give 3x
Put that at the top above the 27x
2x² + 3x
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
Multiply the 3x by the 3x + 4 to get 9x² + 12x,
so write that at the bottom and draw a line:
2x² + 3x
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
9x² + 12x
----------
Now subtract, by mentally changing the signs on
the bottom row. We get 15x, so we write that
at the bottom, and bring down the next term +20:
2x² + 3x
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
9x² + 12x
----------
15x + 20
3x divides into 15x to give 5
Put that at the top above the +20
2x² + 3x + 5
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
9x² + 12x
----------
15x + 20
Multiply the 5 by the 3x + 4 to get 15x + 20,
so write that at the bottom and draw a line:
2x² + 3x + 5
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
9x² + 12x
----------
15x + 20
15x + 20
--------
Now subtract, by mentally changing the signs on
the bottom row. We get 0, so we write that
at the bottom, and we're finished because there
are no more terms to bring down:
2x² + 3x + 5
----------------------
3x + 4 )6x³ + 17x² + 27x + 20
6x³ + 8x²
----------
9x² + 27x
9x² + 12x
----------
15x + 20
15x + 20
--------
0
Edwin