|
Question 716327: What is the square root of 75/27?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!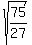 
Here are some steps for square roots of fractions:- ??? (For reasons I'll explain later, I won't tell you this first step until the end.
- If the denominator is not a perfect square, then multiply the numerator and denominator so that denominator becomes a perfect sqaure.
- Use a property of all radicals (including square roots),
 , so the numerator and denominator are in their own "personal" square root. - Simplify the denominator. (It's now the square root of a perfect square so it will simplify to an expression without a square root.)
- Try to simplify the numerator. It may or may not simplify.
- Reduce the fraction, if possible.
Let's see this in action:
2. Make the denominator a perfect square.
27 is not a perfect square. And we can mindlessly turn it into a perfect square by multiplying it (and the numerator by 27). But this makes the numerator a fairly large number. Is there a number smaller than 27 that we can use to turn the denominator into a perfect square? (It doesn't have to be 27 squared. Any perfect square will do, the smaller the better.) If we look at 27 in factored form we can figure this out:
27 = 3 * 3 * 3
Looking at 27 this way we can see that if we had one more factor of 3 we would have two pairs of factors of 3. Since the product of perfect squares is another perfect square, we now know that all we need to do is multiply the numerator and denominator by 3. (It's definitely worth the effort to find these smaller perfect squares when the alternative is a very large number like 27*27!):
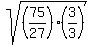
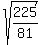
3. Split the square root into a fraction of square roots:
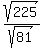
4. Simplify the denominator:
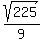
5. Try to simplify the numerator.
You might recognize that the numerator is a perfect square. If not, then start trying to find perfect square factors of 225. 25 is clearly a factor:
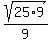
The other factor, 9, is a perfect square factor, too! Now we use another property of radicals,  , to separate the factors:
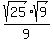
which simplifies...
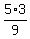
6. Reduce the fraction, if possible.
reduces to
P.S. And now for the mystery first step: 1. Reduce the fraction, if possible. (The same as step 6.) I left this out because it makes this problem very easy and I wanted to show you the full procedure:
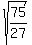
1. Reduce, if possible
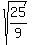
2. Make the denominator a perfect square.
It already is.
3. Split the fraction.
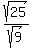
4. Simplify the denominator.
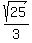
5. Simplify the numerator, if possible.
It's already a perfect square so:
6. Reduce, if possible
5/3 doesn't reduce.
|
|
|
| |
