Question 716214: suppose that log(2) =a and log(3)= b. determine the following by showing your work.
a). log(4)+log(9)
b). log(24)
c. log8 (9)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! The "trick" with these types of problems is to find some way to rewrite the logs you're trying to find in terms of products, quotients and/or powers of the numbers whose logs you know. We are given an expression to use for log(2) and log(3). Plus we should know what the base 10 log of any power of 10 is. So for these problems we will be trying to rewrite the logs in terms of products, quotients and/or powers of of 2's, 3's and/or 10's
a) log(4) + log(9)
It should be easy to see how to rewrite these logs:
Now we can use a property of logs,  , which allows us to move the exponent of an argument out in front:
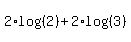
We can replace log(2) with "a" and log(3) with "b":
2a + 2b
b) log(24)
It might take a while to figure out rewrite 24 in terms of 2's, 3's or powers of 10. In factored form 24 = 2*2*2*3 or  :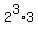
Now we can use another property of logs,  , which allows us to split up the log of a product:
On the first log we can reuse the property we used in part a:
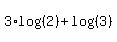
And finally we can replace the log(2) with "a" and the log(3) with b:
3a + b
c)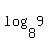 
This one's tricky. This time we have a different base, 8. And since 9 is not a well-known power of 8 we cannot find this log directly. What we will have to do is to use the change of base formula,  , to change this log into base 10 logs so we can use the log(2) and log(3) we were given:
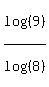
In part a we did log(9) and in part b we did log(8) ( ) so we already know how the numerator and denominator work out:
|
|
|
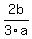
