Question 715531: Hi, I'm Allen and I am dead stuck on this problem. I have found the derivative/slope but am not sure if it's even needed or how to use it. Anyways, I would like to start from scratch. Here is the problem. Thank you!
(1 pt) You will see later that if f(x) = \sqrt x, then f^\prime (4) = 1/4. Use this to find
(a) Use the tangent line approximation at x=4 to f(x) to approximate sqrt4.4
sqrt4.4 ~ _______
(b) Use the tangent line approximation at 4 to f(x) to approximate sqrt9.
sqrt9.9 ~ _______
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! Your referring to a tangent line makes me think you are trying to use the tangent line to find an approximation to a function.
Your function, f(x)=sqrt(x), has a value of 2 at x=4. You also found that the slope of the tangent line at x=4 is  . NOW, you want to actual equation of the line which is tangent to the f(x) at that f(4)=2 value. Point-Slope form will be easiest but no matter, the form of the linear equation is up to you.
The point of tangency is (4,2) and the slope is 1/4. What is the line equation?
Using  , you find  .
(a) Approximately,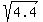 
ONLY an approximation, but it will be near  , or near  .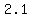
(b) Approximately, what is 
Actually I'm not sure if you wanted that one or for 9.9? I'll do for 9.
Only APPROXIMATELY, ~  , actually not very good.
You see that the farther away from the point of tangency, the worse is this approximation for the function.
|
|
|
