Call the two consecutive integers x and x+1. Their product x*(x+1) or 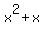 is less than the square of the smaller. The smaller is x, its square is
is less than the square of the smaller. The smaller is x, its square is  and
and 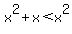
Subtract  from both sides. x<0. Then the larger of the two integers x+1 < 1.
from both sides. x<0. Then the larger of the two integers x+1 < 1.
The problem has many solutions. For example if x=-1 then x+1 = 0 and the product 0*1 = 0 is less than the smaller squared = -1 squared = 1. 0 < 1.
If x=-10, then x+1 = -9. Product: 90. Smaller squared = 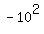 = 100.
= 100.
Let's try an x outside the solution, and as a result an x+1 outside the solution.
If x=0 then x+1 = 1. 0*1=0 and 0 squared = 0. The product is not less than the smaller number squared. That's what we expect since x+1 < 1 is the solution.
Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)