Question 715068: If we have a box containing slips of paper with the following numbers: 3,5,8,10,13,23,30,36,21,34 and a slip of paper is selected and not replaced. What are the following probabilities:
p(multiple of 3 then multiple of 5)
P(prime then odd)
P(prime then even then 21)
P(odd then 10 then 30)
How do you deal with numbers that share a common property (I.e. multiple of 5 and three, or odd and prime) in an independent probability problem like this one.
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website! If we have a box containing slips of paper with the following numbers: 3,5,8,10,13,23,30,36,21,34 and a slip of paper is selected and not replaced. What are the following probabilities:
p(multiple of 3 then multiple of 5) =
P(one of these 4, {3,30,36,21) AND THEN one of these 3 {5,10,30}.
This breaks into two cases each with a different probability:
Case 1: We draw the 30 first    = 
Case 2: We don't draw 30 first   =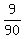 
Desired probability =  = 
--------------------------
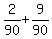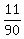P(prime then odd)
P(one of these 4, {3,5,13,23) AND THEN one of these 5 {3,5,13,23,21}.
This breaks into two cases each with a different probability:
Case 1: We draw the 21 second   =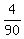 
Case 2: We don't draw 21 second = 
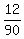Desired probability =  =  = 
-------------------------------------
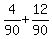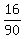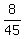P(prime then even then 21)
p(one of these 4, {3,5,13,23) AND THEN one of these 5 {8,10,30,36,34} and THEN {21}
None of these have a common property so it is not necessary to break into
cases:
Desired probability =   =  =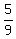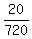 
-----------------------------------------
P(odd then 10 then 30)
p(one of these 5, {3,5,13,23,21}. AND THEN {10} AND THEN {30}
None of these have a common property so it is not necessary to break into
cases:
Desired probability =  =  =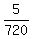 
How do you deal with numbers that share a common property (I.e. multiple of 5 and three, or odd and prime) in an independent probability problem like this one.
We have to break them into two or more cases, cases where we choose ones
with the common properties, and cases where we don't. Then add the probabilities.
Edwin
|
|
|
