Question 714460: I need help on this questions!
Find an equation of the line that passes through the point (-1,3) and is parallel to the line passing through the points (-2,-3) and (2,5).
Find an equation of the line that passes through the point (1,-2) and is perpendicular to the line passing through the point (-2,-1) and (4,3).
Answer by Edwin McCravy(20064)   (Show Source):
You can put this solution on YOUR website! I need help on this questions!
Find an equation of the line that passes through the point (-1,3) and is parallel to the line passing through the points (-2,-3) and (2,5).
We want to find the equation of the green line through (-1,3).
We know that it has the SAME slope as the red line thru (-2,-3) and (2,5).
So we find the slope of the red line using the slope formula:
m = 
where (x1,y1) = (-2,-3)
and where (x2,y2) = (2,5)
m = 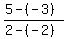 =  =  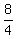= 2
So the slope of the green line is also 2.
Next we use the point-slope formula:
y - y1 = m(x - x1) where (x1,y1) = (-1,3)
y - 3 = 2(x - (-1))
y - 3 = 2(x + 1)
y - 3 = 2x + 2
y = 2x + 5
That's it.
-------------------------------------------------
Find an equation of the line that passes through the point (1,-2) and is perpendicular to the line passing through the point (-2,-1) and (4,3).
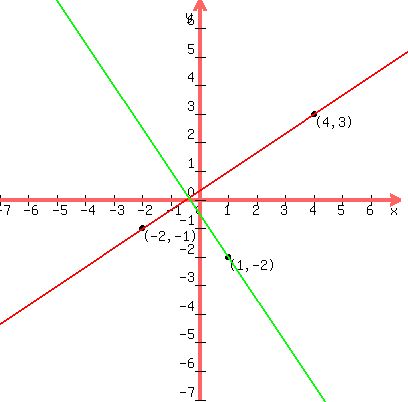
We want to find the equation of the green line through (1,-2).
We know that it has the NEGATIVE RECIPROCAL of the slope of the red line
thru (-2,-1) and (4,3).
So we find the slope of the red line using the slope formula:
m =
where (x1,y1) = (-2,-1)
and where (x2,y2) = (4,3)
m =  =  =  =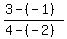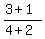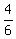 
So the slope of the green line is the NEGATIVE RECIPROCAL of ,
which is  .
Next we use the point-slope formula:
y - y1 = m(x - x1) where (x1,y1) = (1,-2)
y - (-2) = (x - 1)
y + 2 = (x - 1)
Clear the fraction by multiplying through by 2
2y + 4 = -3(x - 1)
2y + 4 = -3x + 3
2y = -3x - 1
Divide through by 2
y = x - 
That's it.
PARALLEL LINES HAVE THE SAME SLOPE.
PERPENDICULAR LINES HAVE SLOPES WHICH ARE THE
NEGATIVE RECIPROCALS OF EACH OTHER.
Edwin
|
|
|
