|
Question 714329: What two numbers are twice as far from 40 as they are from 70
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE FIFTH GRADER WAY:
That number could be in between 40 and 70,
or could be larger than 70.
(It cannot be less than 40 because that would put it close to 40 than to 70).
If it's in between, it should be  of the way from 40 to 70, of the way from 40 to 70,
so you have gone 2 thirds of the way, but you have 1 third of the way to go.
Since that way is  , ,  of that way is of that way is  , and , and
 of that is of that is  . .
The number between 40 and 70, that is 10 away from 70, and
 away from away from  is is
 . .
If the number is larger than 70, and
going from 40 to that number is twice as far as
going from 70 to that number,
then 70 is half way there, and the distance from 40 to 70,
 , ,
is the same as from  further to the number, further to the number,
so the number is  past past  . .
It is 
TWO WAYS THAT LOOK MORE LIKE ALGEBRA:
A number  is is
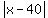 from from  and and
 from from  . .
We know that

At this point,
we can just square both sides of the equal sign and worry about eliminating any possible extraneous solution later.
Or we could examine what those absolute values could be and work for each case.
Squaring both sides we get
 --> -->  --> -->  --> -->  --> --> 
Dividing both sides by 3 we get

If we are good at factoring, we factor to get
 with solutions with solutions
 and and 
If we cannot factor, we apply the quadratic formula:


 --> --> 
with solutions
 --> -->  --> -->  and and
 --> -->  --> -->  . .
Examining case by case the absolute values:
For 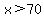 , ,
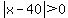 so so  and and
 so so 
 transforms into transforms into
 --> -->  --> -->  --> -->  --> --> 
For 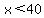 , ,
 so so  and and
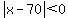 so so 
 transforms into transforms into
 and multiplying times and multiplying times  both sides of the equal sign we get both sides of the equal sign we get
 as above, as above,
which gives us the solution  as above, as above,
but as we had started with 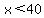 , ,
we did not find a solution that fit the case 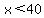 . .
For  such that such that 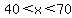 , ,
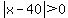 so so  and and
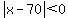 so so 
 transforms into transforms into
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  . .
|
|
|
| |