Question 714020: If angle AOP is an acute angle and the circle, centre O, of radius 10 cm is drawn. Calculate the angle AOP such that area of triangle OAP= Area of circle/ 5π
What i did:
Drew a diagram (probably wrong so is my working)
π x radius squared
= π x 10 squared
= 314.1592654
= 314.16 (2dp)
area of triangle OAP= area of circle/ 5 π
= 3.1416/5 π
= 19.739 (2dp)
Area of triangle = 1/2 x b x h
197.39= 1/2 x 10 x h
= 5h
h= 39.478
Ɵ= inverse tan 39.478/5
= 82. 78
Which is WAY off what the actual answer should be..
Please Help! Thanks!
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I strongly suspect that it is the area of sector AOP, not the area of triangle AOP that is the area of the circle divided by 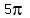 . The reason for my suspicion is that the problem, as you posted it, has two solutions and is quite difficult. I will solve the what I think the problem is first. Then I will solve the problem as you posted it. . The reason for my suspicion is that the problem, as you posted it, has two solutions and is quite difficult. I will solve the what I think the problem is first. Then I will solve the problem as you posted it.
Angle AOP is called a central angle because its vertex is at the center of a circle. There is a proportion that will always be true that connects the measure of a central angle with the area of the sector it creates:
measure of central angle = area of the sector formed
360 degrees area of the circleLet's call the measure of angle AOP "x". The area of the circle will be  And the area of the sector is the area of the circle divided by 5pi: And the area of the sector is the area of the circle divided by 5pi:  Substituting these into the proportion we get: Substituting these into the proportion we get:

Reducing the fraction:

Multiplying by 360:

This is the number of degrees in angle AOP. If you want/need this in decimal form, get out your calculator. (Note: If we measure the angle in radians, this would be:  radians.) If either of these is the correct answer, then you don't need to keep reading, although you might learn something if you do. radians.) If either of these is the correct answer, then you don't need to keep reading, although you might learn something if you do.
Solving the problem as posted...
First let's get a diagram:- Draw a circle and label the center of the circle "O".
- Label a point on the circle as "A" and label another point on the circle "P". Make A and P close enough to each other that angle AOP appears to be acute.
- Since OA and OP are radii, label their lengths as 10's
- Draw a segment from A to P.
- Draw a perpendicular segment from O to segment AP. O is one endpoint of this new segment. Label the other endpoint of this new segment (on AP) as "Q".
If these instructions have been clear, you should now have:- A circle with center O
- Triangle AOP
- Two right triangles: AQO and PQO
Now let's try to solve this problem.
Your work is OK until you use the area of a triangle formula. Although by using a decimal for  you end up with an area that is a little but wrong. You could probably still get an acceptably close answer with this slightly wrong area but look what happens if you don't use a decimal for you end up with an area that is a little but wrong. You could probably still get an acceptably close answer with this slightly wrong area but look what happens if you don't use a decimal for  : :
Area of the circle = 
Area of triangle AOP = 
Now we get to where you went seriously wrong. The area of a triangle is (1/2)*b*h. When you use this formula, the base can be any side of the triangle. But the "h" is specific to to each base. The height is a segment from the remote vertex which is perpendicular to the line containing the base. If you want to use a 10 for the base, let's say OA, then the height would be a segment from P which is perpendicular to OA. This segment is not in our picture. And even if it was, we would not use the inverse tan on it. We would have to use the inverse tan on h/(the length of the segment from O to where the height intersects with OA (which we do not know)).
To finish the solution we are going to go in a different direction. The two right triangles, AQO and PQO, are congruent for reasons I hope you see. (If not, I'll explain later.) And their areas add up to the area of triangle AOP. So the area of each of these right triangles will be 1/2 of the area of triangle AOP, 10. We are going to use the area formula for a triangle on one of these right triangles, lets' say AOQ. With right triangles you can use the two legs as a base and a height. We do not know what either of the legs, AQ and OQ, are but we do know the length of the hypotenuse, OA. If we call the length of leg AQ "x", then we can use the Pythagorean Theorem to find an expression for the length of leg QO: 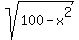
Now let's put these expressions for the legs into our area formula:
Area of triangle AQO = 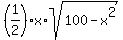
We know that this area is 10 so:

Now we solve for x. Multiplying both sides by 2 eliminates the fraction:

Squaring both sides eliminates the square root:

which simplifies to:

Subtracting the entire right side we get:

Unfortunately this will not factor. But it is in quadratic form (because the first exponent is twice the second one) so we can use the Quadratic Formula:

Simplifying...




which is short for:
 or or 
Using our calculators...
 or or 
 or or 
 or or 
Square root of each side:
x = 9.79 or x = 2.04
The fact that there are two solutions for x will lead to two solutions for the angle. This is why I suspect that it was the area of sector AOP that was the (area of circle/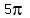 ), not the area of triangle AOP. To find angle AOP we will first find angle AOQ. And since the two right triangles are congruent, twice angle AOQ will be angle AOP. ), not the area of triangle AOP. To find angle AOP we will first find angle AOQ. And since the two right triangles are congruent, twice angle AOQ will be angle AOP.
To find angle AOQ we will use inverse tan on x/10:
Angle AOQ = 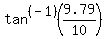 or Angle AOQ = or Angle AOQ = 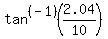
Angle AOQ = 44.39 or Angle AOQ = 11.53
Angle AOP = 88.78 or Angle AOP = 23.06
P.S. Why the two right triangles are congruent:- Triangle AOP is isosceles since OA = OP.
- Angles OAP and OPA are congruent since the angles opposite the congruent sides in an isosceles triangle are congruent.
- Angles OAP is in one of the right triangles and angle OPA is in the other.
- Angles AOQ and POQ are congruent because the other two angles of each triangle are congruent.
- By ASA the two triangles are congruent
|
|
|