Question 714016: The fourth, seventh and sixteenth terms of arithmetic series form a geometric series. If the first six terms of arithmetic series have a sum of 12.
(a) Find the common difference of the arithmetic series
(b) Calculate the common ratio of the geometric series
Answer by kevwill(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! If x is the value of the first term, and d is the difference between terms, then the first 6 terms of the arithmetic series are:
 , , 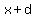 , , 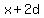 , , 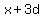 , , 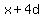 , , 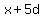
The sum of these 6 terms is 12, so we have:

The 4rd, 7th, and 16th terms, a geometric series, are
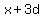 , , 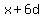 , and , and 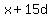
So we know that

Multiplying both sides by 




 where where  (If (If  we have the trivial sequence we have the trivial sequence  , ,  , ,  , ,  , ,  , ...) , ...)
Plugging  into into 




And plugging  into into 




So our series is:
 , ,  , ,  , ,  , ,  , ,  , ... , ...
The 4th, 7th, and 16th terms are  , ,  , and , and 
So the difference in the arithmetic sequence is 2 and the ratio in the geometric sequence is 3.
|
|
|