If two fair number cubes are rolled, what is P(1 and 2)?
That means the probability of getting one of these 2 rolls:
(1,2) (2,1)
out of these 36 rolls:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
That's a probability of 2 out of 36 or 
which reduces to 
--------------------------------------
If two fair number cubes are rolled, what is P(1 and 2)?
That means the probability of getting one of these 18 rolls:
(1,2) (1,4) (1,6)
(2,1) (2,3) (2,5) (3,2) (3,4) (3,6)
(4,1) (4,3) (4,5) (5,2) (5,4) (5,6)
(6,1) (6,3) (6,5)
out of these 36 rolls:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
That's a probability of 18 out of 36 or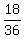 
which reduces to 
(