Question 713915: A cheese manufacturer combines Romano cheese that costs $4.00 per pound with aged Parmesan cheese which costs $7.00 per pound to make 30 lbs of a grated cheese mixture. How many pounds of each cheese should they include if they want the 30 ound mixture to cost $5.70 per pound?
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! The manufacturer wants to mix some high strength cheese with so low strength cheese and have a known quantity of mixture of a known intermediate strength cheese. Strength here is money, price (some expected dollars per pound).
M=pounds of mixture, 30 pounds.
u= amount of low strength, unknown pounds
v= amount of high strength cheese, unknown pounds
L = strength of the low strength cheese, $4/pound
H = high strength cheese, $7/pound
T = Target price per pound 5.70
Setup Equations.
Solve for u and v.
Sometimes the values given are conveniently chosen to make the solving easy, but you don't want to always rely on that.
and
How neat those numbers will be, we not know (unless we substitute them NOW).
v=M-u, so keep going in symbols, subsituting this one into the percents equation:
Might be most convenient if done symbolically to use
 , which was multiplied by 
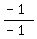
and
 , since you just found u.
Substitute Values to determine values of u and v.
 , which you compute and then find the value for v.
|
|
|
