Question 713510: Solve for x to three significant digits
3^2x-7 X 3^x + 10 = 0
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! First of all, I assume the equation is:
If this is correct, then in the future please- put multiple-character exponents (like 2x) in parentheses. What you posted meant
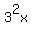 - use an asterisk, "*" to indicate multiplication, not an x (especially when there are variable x's in the expression)
If my assumption is not correct then you'll have to re-post your problem because I'm going to solve my version of the equation.
With the exponent on the first 3 being exactly twice the exponent, this equation is in what is called "quadratic form". Quadratic form equations can be solved in much the same way as regular quadratic equations are solved.
Until you have solved a few of these quadratic form equations it can be easier to use a temporary variable. Make the temporary variable equal to the base and smaller exponent:
Let 
Then 
Substituting these into our equation we get:
This is obviously a quadratic equation. It is already in standard  form. So we solve it by factoring (or by using the Quadratic Formula). This factors quite easily:
(q-5)(q-2) = 0
From the Zero Product Property we know that:
q - 5 = 0 or q - 2 = 0
Solving these we get:
q = 5 or q = 2
Of course we are interested in solutions for x, not for q. So we substitute back in for q:
 or 
We have some more work to do to solve for x. Since 5 and 2 are not obvious powers of 3 and since 3, 5 and 2 are not obvious powers of some third number, we will have to use logarithms to solve for x. Logarithms of any base may be used. However there are advantages to choosing certain bases:- Choosing the logarithm's base to match the exponent's base will result in the simplest possible exact expression for the solution.
- Choosing the logarithm's base to match a base your calculator "knows", base 10 ("log") or base e ("ln"), will result in an expression that can be easily entered into our calculators is a decimal approximation is needed/desired.
Since the problem asks for a rounded decimal ("to three significant digits" implies that there should just be digits, no logarithms), we will choose the logarithm's base to be log or ln. I'll choose ln. So we'll find the ln of each side of both equations:
 or 
The next step is to use a property of logarithms,  , which allows us to move the exponent of the argument of a log out in front of the log. (It is this property that is the very reason we use logarithms on equations like  . It allows us to move an exponent, where the variable is, out in front where we can "get at" the variable with "regular" algebra.) Using this property on both equations we get:
 or 
Next we divide both sides of both equations by ln(3):
 or 
These are exact expressions for the solution to your original equation. I'll leave it up to you to use your calculator to get decimal answers and then to round that to three significant digits. Just be sure to find the two logs in each equation first and then divide. Do not, for example, find ln(5/3).
P.S. Once you've done a few of these quadratic form equations you will no longer need to use a temporary variable. You will be able to see how to go directly from
to
to
or
etc.
|
|
|
