Question 713489: Suppose that during a test drive of two cars, one car travels 196 miles in the same time that the second car travels 140 miles. If the speed of one car is 16 miles per hour faster than the speed of the second car, find the speed of both cars.
The speed of the first car is __ mph, and the speed of the second car is __ mph.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I can think of many ways to solve the problem that make sense to me.
With some luck, at least one of those ways will make sense to you.
If you are expected to show and explain your work, there may be one way that is expected, or preferred.
In that case, I hope that the teacher understands that any way to solve a problem is a good way to solve it.
THE FIFTH GRADER WAY:
An extra 16 mph (miles per hour) resulted in an extra 56 miles (196-140=156) for the first car.
Then the time for that long test drive (in hours) must have been

The test drive took 3.5 hours.
The speed of the first car (in mph) was
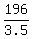 miles per hour. miles per hour.
The speed of the second car (in mph) was
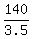 miles per hour. miles per hour.
With a calculator those division are easy to do.
Without a calculator, I can calculate it easier by first multiplying numerator and denominator times 2:


THE ALGEBRA WAY WITH ONE VARIABLE:
 = speed of the slower second car (in mph, miles per hour) = speed of the slower second car (in mph, miles per hour)
 = speed of the faster first car (in mph, miles per hour) = speed of the faster first car (in mph, miles per hour)
The time it took for each car to complete the test can be calculated as the distance covered, divided by the speed,
Since it was the same for both cars,
 --> --> 
Possible explanations for that step:
They are equivalent equations, and if we have to "show our work" more clearly
we use whatever explanation/justification the teacher thinks is needed.
If we studied proportions we say that the equation above is a proportion,
and if we were told that to solve proportions we
"equate the cross products" we just "cross-multiply" and write

Otherwise we say that we get to  by "eliminating denominators", by "eliminating denominators",
and we do that by multiplying both sides of the equal sign times  and times and times 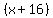 in two steps, or multiply times both together in one step, multiplying times in two steps, or multiply times both together in one step, multiplying times  . .
Then,
 --> -->  --> -->  --> -->  --> -->  --> --> 
and 
ONE ALGEBRA WAY WITH TWO VARIABLES:
 = speed of the slower second car (in mph, miles per hour) = speed of the slower second car (in mph, miles per hour)
 = speed of the faster first car (in mph, miles per hour) = speed of the faster first car (in mph, miles per hour)
 time that each car took to complete the test drive (in hours). time that each car took to complete the test drive (in hours).
 is the distance covered by the slower second car (in miles) is the distance covered by the slower second car (in miles)
 --> -->  is the distance covered by the faster first car (in miles) is the distance covered by the faster first car (in miles)
We can solve the system 
by just plugging into the second equation the value for 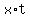 from the first equation to get from the first equation to get
 --> -->  --> -->  --> -->  --> --> 
Then we plug that value into the first equation,  , to get , to get
 --> -->  --> --> 
and 
ANOTHER ALGEBRA WAY WITH TWO VARIABLES:
We need names for the variables, and when using two variables we should be allowed to use any name we want. I'll use names that make it easier to remember what we are talking about. Feel free to choose any name you like (as long as you don't think the teacher will object).
 = speed of First (or Faster) car = speed of First (or Faster) car
 = speed of Second (or Slower) car = speed of Second (or Slower) car
We know that 
and we can figure out that, since  was the same for both cars, was the same for both cars,
 <--> <-->  . .
Then we can solve the system 
Substituting the expression for  into the second equation. into the second equation.
 --> -->  --> -->  --> -->  --> -->  --> -->  --> --> 
|
|
|