Question 713154: Suppose a boat has a speed in still water of 10 mph. The boat travels 48 miles upstream and then makes the 48 mile return trip downstream, in a total travel time of 10 hours. What is the speed of the river? - (I don't know how to assemble this information in a table or how to write it into an equation)
Answer by kevwill(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let s be the speed of the river. Then traveling upstream, the boat's net speed is 10-s mph, and traveling downstream, the boat's net speed is 10+s mph.
For time-speed-distance problems, time is equal to distance/speed. We know the distance upstream is 48 miles and the speed is (10-s) miles per hour, so the time to go upstream is
 hours hours
Likewise, the distance downstream is also 48 miles, but this time the speed is (10+s) miles per hour. So the time to go back downstream is
 hours hours
The total round trip (t1 + t2) is 10 hours, so we have:

Multiplying both sides by 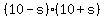 gives gives





 or or 
In this case s=-2 just means that the river is flowing in the opposite direction and we actually went downstream first, then back upstream. In either case, the speed of the river is the same: 2 mph
|
|
|