Question 7129: You are creating a window display at a toy store
using wooden blocks. The display involves stacking blocks in triangular forms.
You begin the display with 1 block, which is your first “triangle,” and then stack
3 blocks, two on the bottom and one on the top, to get the next triangle. You
create the next three triangles by stacking 6 blocks, then 10 blocks, and then
15 blocks. How many blocks will you need for the ninth triangle?
I can find the answer by counting fine... it is 45... I can't remember how to write the equation though. I know it is exponential & it looks something like this... n^(n-1) can you please help me?
Answer by glabow(165)   (Show Source): (Show Source):
You can put this solution on YOUR website! A note on this: Carl Frederick Gauss is said to have solved this as a small child when a teacher gave the problem to keep the kiddies quiet for a long time. He did it quickly with the following insight:
Suppose you build a second triangle next to the first one, only you build it upside down. The row of blocks on the bottom of a triangle will match up with the single block of the upside down triangle. The next to bottom row will match up with the second row of the upside down triangle.
The insight is that each row of the two triangles (one right side up, one up side down) will add up to one more than the number of the triangle. Pictorially it looks like this:
x xxxxx
xx xxxx
xxx xxx
xxxx xx
xxxxx x
Notice that each row of the combined triangles will add up to n+1 (where it is triangle number n).
Since there will be n rows for a triange of n blocks, the total blocks in two triangles is n(n+1). But since you will only have one of each triangle, you divide by 2.
The number of blocks in a triangle of base size n is found to be
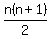
This is a slight modification of the problem given to little Gauss, but it actually the same issue.
|
|
|