|
Question 71263This question is from textbook Beginning Algebra
: Multiply the following functions.
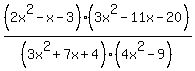
I have been trying to solve this problem and an having troble figuring this one out. I need some help. Thanks
This question is from textbook Beginning Algebra
Found 2 solutions by Earlsdon, bucky:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! These are book problems, so they are usually "nice" problems that are designed and set up to teach you about a skill. In this case, the problem is to teach you to look for common factors in the numerator and denominator. If you find a factor in the numerator that is common with one in the denominator, you can cancel them out.
.
What you need to do here is factor the two expressions in the numerator and then factor the two expressions in the denominator and look for common ones.
.
Without going into a lesson on how to factor, let me just give you the factors for each expression and then you can see how the cancellation process works. But you need to understand how to factor or you will unable to work problems such as these.
.
In the numerator 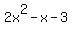 factors into factors into 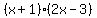 . Also in the numerator . Also in the numerator 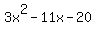 factors into factors into 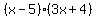 . .
.
In the denominator 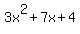 factors into factors into  and and 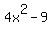 factors into factors into 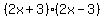 . [Notice that the last one here is in the form of the difference of two squares. Just take the square root of the two terms and then set them up as the sum and the difference of the square roots multiplied by each other.] . [Notice that the last one here is in the form of the difference of two squares. Just take the square root of the two terms and then set them up as the sum and the difference of the square roots multiplied by each other.]
.
So if you substitute the factors into their corresponding places in the numerator and denominator your problem becomes:
.
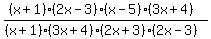
.
Notice that there is an x+1 factor in the numerator and a x+1 factor in the denominator. Cross them out. The same thing goes for the 2x-3 factor in the numerator and the 2x-3 factor in the denominator. And again, the same thing goes for the 3x+4 factor in the numerator and the 3x+4 factor in the denominator.
.
When you are done doing all three cancellations, what you are left with is x-5 in the numerator and 2x+3 in the denominator. So the answer to this problem is:
.
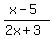
.
Hope this helps you to understand the importance of trying to factor the expressions and then to look for common factors in the numerator and denominator. As a clue, once you find a set of factors for one expression, see if they are a hint to finding other factors. For example, you could have found the factors to 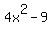 rather easily had you recognized the "pattern" as being the difference of two squares. The factors were rather easily had you recognized the "pattern" as being the difference of two squares. The factors were 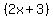 and and 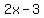 . So you might have looked in the numerator and guessed that one of those two factors in the numerator was likely a factor of . So you might have looked in the numerator and guessed that one of those two factors in the numerator was likely a factor of  in the numerator. Then when you find that in the numerator. Then when you find that 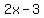 was a factor of was a factor of  and and  was its other factor, you might guess that was its other factor, you might guess that  was also a factor of was also a factor of 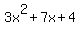 in the denominator. And so on. Otherwise, you can just use the trial and error system of factoring. If you are familiar with the quadratic formula, you can also use it to factor a quadratic, but that's a whole 'nuther lesson. in the denominator. And so on. Otherwise, you can just use the trial and error system of factoring. If you are familiar with the quadratic formula, you can also use it to factor a quadratic, but that's a whole 'nuther lesson.
|
|
|
| |