Question 7125: Solve the inequality x^2-5x+6>0. State the solution set using interval notation and graph it. Any help is greatly appreciated.
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, you would factor the trinomial on the left side of the >. We'll have to get that inequality to say something like (x ± ?)(x ± ?) > 0. So, what times what = 6 that has a sum or a difference of -5? It turns out to be 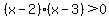
By looking at the factored inequality, you can pick out the "solutions" to be 2 and 3. Since its an inequality, the true solutions will be a range in the number line. The 2 and the 3 are just your critical points. Since the inequality is a >, you would draw open circles at 2 and at 3 on the number line.
The two open circles divide the number line into three intervals: (-∞,2),(2,3) and (3,∞). So, which of these intervals is a solution to your inequality? We'll have to attempt a series of trial and error.
Let's take the (-∞,2) and choose a random number in that range. Let's pick 0 because it seems easiest, and plug it into the inequality. (0 - 2)(0 - 3) ?> 0. It turns out that 6 > 0 which is true. Just because the 0 passed the inequality, so will ALL values in the interval (-∞,2). So, (-∞,2) is a solution.
Let's take the (2,3) and choose a random number in that range, say 2.5, smack in the middle. Let's plug it in: (2.5 - 2)(2.5 - 3) ?> 0 ---> (0.5)(-0.5) ?> 0 fails because the left side gave us a negative number, definitely not greater than 0. Just because the 2.5 failed, so will ALL the other values in the range (2,3). So (2,3) is not a solution to the inequality.
What about the (3,∞)? Let's pick the value 4 and plug it in to see if it will work. (4 - 2)(4 - 3) ?> 0 ---> (2)(1) ?> 0 turns out to be true. So, just because the 4 passed the inequality and is in the range (3,∞), (3,∞) is a solution set of your inequality.
So two intervals make up the solution to your inequality: (-∞,2) and (3,∞). They might even want you to write it as (-∞,2) U (3,∞).
|
|
|