|
Question 712412: 1.) (6+5v)(36-25v^2)and (6-5v) LCM?
2.)7/2V+5 THE RATIONAL EXPRESSION IS NOT DEFINED FOR V= ?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) To find the least common multiple (LCM) you must know what the factors of the expressions are. So we start by factoring (6+5v), (36-25v^2)and (6-5v)
(6+5v) = 1 * (6+5v)
(36-25v^2) = 1 * (6+5v) * (6-5v) [A difference of squares]
(6-5v) = 1 * (6-5v)
LCM (or LCD) = 1 * (6+5v) * (6-5v) I've factored these expressions in this way on purpose. Using spacing, I ensured that the factors in each column were the same. (I'll explain the 1's later.) With the factors arranged this way, the LCM will be the product of the factors from each column. Use only one factor from each column. The LCM here would be:
1 * (6+5v) * (6-5v) = 36-25v^2
2) Expressions can be undefined for a variety of reasons. But for the expression 7/2V+5 there is only one reason: a zero denominator. 7/2V+5 will be undefined for any value of V that makes the denominator zero. Since I cannot tell if the denominator is 2V or 2V+5 you will have to figure this out yourself. Just set the denominator, whatever it is, equal to zero and solve for V. That will tell you the value of V that will make the expression undefined. [If the denominator is 2V+5 as I suspect, then please use parentheses around multiple-term denominators (or numerators): 7/(2V+5)]
P.S. The way I arranged the factors to find the LCM can also be used to find greatest common factors (GCF's). The 1's in the list of factors are not needed to find LCM's but they can be necessary to find a GCF. To use the table of factors above to find the GCF of those three expressions, you use factors that are present in every row. In this case, only the 1's are present in every row. So the GCF is a 1. (If there had been other factors in every row then the GCF would be the product of the 1 and these other factors.)
P.P.S. Least common denominators (LCD's) are simply the LCM of some denominators so you can use the table of factors to find LCD's, too. A frequent use of LCD's is to be able to add or subtract fractions. In this case using a table of factors like the one above can not only tell you what the LCD is but it can also be used to tell you what each fraction needs to be multiplied by to make its denominator equal to the LCD. For example, let's say you wanted to add:
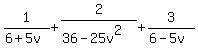
Using the table above we would find that the LCD is 36-25v^2. And it is perhaps obvious that the second fraction is fine as it is. But for the other fractions we have to change them so that their denominators match the LCD. Looking at the table we can compare the factors of each denominator with the factors of the LCM/LCD and see what is missing. The first fraction's denominator is "missing" a factor of (6-5v) and the last fraction's denominator is "missing" a factor of (6+5v). This tells us what to multiply each fraction by:
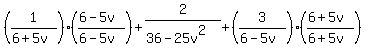
etc.
|
|
|
| |