|
Question 712178: Simplify. Assume that variables can represent any value
square root of (25x^2+30x+9)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
Simplifying square roots involves trying to find perfect square factors of the radicand. (The expression inside a radical is called a radicand.) So we start by factoring the radicand.
The radicand fits the pattern of one of our factoring patterns:
The first term of the pattern is a perfect square. The first term of our radicand is also a perfect square:  . The last term of the pattern is also a perfect square. The last term of our radicand is a perfect square, 3 squared. The middle term of the pattern, 2ab, is 2 times what is being squared in the first term time what is being squared in the last term. The middle term of our radicand is equal to 2 times 5x (what is being squared in front) times 3 (what is being squared in back. So the radicand does fit the pattern with "a" being "5x" and "b" being 3. So according to the pattern we the radicand will factor into  :
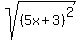
As we can see, not only do we have a factor that is a perfect square, the whole radicand turned out to be a perfect square!
An easy temptation is to think that the square root simplifies to just 5x+3. But every positive number has two square roots, a positive one and a negative one. A square root without a minus in front of it is a reference to the positive square root. So our original square root, , is a reference to the positive square root of  . So when we are done simplifying we must have an expression that is just as guaranteed to be positive as the original square root! We are told that x could represent any value. So 5x+3 could be any value, too, including negative. To ensure the "positiveness" of our simplified answer we use absolute value. So
simplifies to:
|
|
|
| |
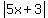
