Question 712038: Write a fourth degree polynomial equation with integer coefficients that has two irrational roots and two imaginary roots.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! If our 4 roots are  , ,  , ,  , , 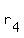 then our polynomial, in factored form, will be: then our polynomial, in factored form, will be:

where "a" can be any non-zero number. To find the polynomial we will:- Pick the 4 roots
- Pick a number for "a"
- Multiply out the factored form and then simplify.
1. Pick the roots.
This will be the hardest part. Lets say that  and and  will be our irrational roots of the polynomial. Most of the irrational numbers you know are roots (square, cube, 4th, etc.). To get integer coefficients the problem specifies, we need the two factors with these roots, will be our irrational roots of the polynomial. Most of the irrational numbers you know are roots (square, cube, 4th, etc.). To get integer coefficients the problem specifies, we need the two factors with these roots, 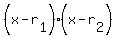 , to multiply in such a way that the radicals disappear. , to multiply in such a way that the radicals disappear. 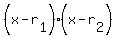 is the product of two binomials (two-term expression). So we want the product of two binomials which include radicals to result in something where there are no radicals. The key to figuring this out is the factoring pattern: is the product of two binomials (two-term expression). So we want the product of two binomials which include radicals to result in something where there are no radicals. The key to figuring this out is the factoring pattern:

This shows us how two binomials can be multiplied and result in an expression of perfect squares. If we make our irrational roots be square roots then we can get rid of the radicals by using this pattern to get perfect square terms. But which square roots? Since the factors of our polynomial are written as subtractions, let's rewrite the pattern as subtractions:

So we want our square roots to be "-b" and "b". In other words, we want square roots that are opposites. So we can use  and and  , or , or  and and  , or , or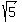 and and  , etc. Let's pick , etc. Let's pick  and and  . So our polynomial, at this point is: . So our polynomial, at this point is:

or

The imaginary roots of the polynomial will have an "i" in them. "i", as you should know, is 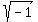 . Since i is a square root, we can use the exact same logic for picking these roots as we did for the irrational roots. So for the imaginary roots we want opposites, too. Let's pick i and -i. Now our polynomial is: . Since i is a square root, we can use the exact same logic for picking these roots as we did for the irrational roots. So for the imaginary roots we want opposites, too. Let's pick i and -i. Now our polynomial is:

or

2. Pick a value for "a".
The only rule is that you can't pick zero. Let's be easy on ourselves and pick 1. So our the complete polynomial, in factored form, is:

or

3. Multiply.
Multiplying the first two factors is easy since we can use the pattern:

which simplifies to:

We can multiply the last two factors using the pattern, too. (Remember, with multiplication you can multiply in any order you choose.)

which simplifies to:

Since  this further simplifies: this further simplifies:


One more multiplication. No pattern can be used. We must use FOIL:

which simplifies:


or

This is a 4th degree polynomial with integer coefficients with two irrational roots,  and and  , and two imaginary roots, i and -i. , and two imaginary roots, i and -i.
You can check each root by replacing the x with that root and see if P(x) is zero. If it is then that root is good.
|
|
|