SOLUTION: Hi. My name is Allen and I've been having difficulty with this problem. I sent this equation to this website a few days ago but no response. I came up with 7/9 hours, which is inco

Algebra ->  Equations -> SOLUTION: Hi. My name is Allen and I've been having difficulty with this problem. I sent this equation to this website a few days ago but no response. I came up with 7/9 hours, which is inco      Log On


   

Question 711800: Hi. My name is Allen and I've been having difficulty with this problem. I sent this equation to this website a few days ago but no response. I came up with 7/9 hours, which is incorrect. Here is the equation:
A swimming pool can be filled by either or both of two pipes of different diameters. It takes the smaller pipe twice the time that the larger pipe takes to fill the pool. If water flows through both pipes it take 2 1/3 hours to fill the pool. How long will it take the larger pipe to fill the pool? [hint: let x be the amount of the pool filled by the small pipe in one hour]
Time = ______ hours
Thank you!
Found 3 solutions by jim_thompson5910, solver91311, josgarithmetic:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
I'm going to make x = time it takes larger pipe to fill the pool on its own.

----------------------------

2 1/3 = 2+1/3

2 1/3 = 6/3 + 1/3

2 1/3 = 7/3

---------------------------

1/x + 1/(2x) = 1/(7/3)

2/(2x) + 1/(2x) = 3/7

3/(2x) = 3/7

3*7 = 3*2x

21 = 6x

6x = 21

x = 21/6

x = 7/2

So it will take 7/2 hours or 3.5 hours for the larger pipe to fill the pool on its own.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Let represent the number of hours it takes for the larger pipe to fill the pool. That means that the larger pipe can fill th of the pool in one hour. Likewise, the smaller pipe, that takes hours to fill the pool, can fill of the pool in one hour. Working together, they fill the pool in hours, or hours. That means that the two pipes working together can fill of the pool in one hour. Since what one of the pipes can do in one hour plus what the other pipe can do in one hour is equal to what they can do together in one hour, we can say:



Solve for

John

Egw to Beta kai to Sigma
My calculator said it, I believe it, that settles it
The Out Campaign: Scarlet Letter of Atheism

Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Let r = filling rate of the large pipe.
It takes the smaller pipe twice the time that the larger pipe takes to fill the pool.

That means, filling rate for the small pipe is 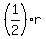%281%2F2%29r.

If water flows through both pipes it take 2 1/3 hours to fill the pool.
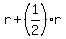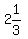Both pipes open and filling the pool at the same time means that the fill rate is r%2B%281%2F2%29r. At this extent of information development, you could create a table of data but this is not really necessary. You are given the time it takes to DO THE JOB of filling the tank, being 2%261%2F3 hours.

Pipe___________rate_______________time____________how many jobs
Small___________r%2F2_______________(____)___________1
Big_____________r_________________(____)___________1
Both Together___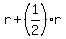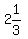r%2B%281%2F2%29r_____________2%261%2F3_____________1

If the rate is number of jobs per unit of time, and if time is time (be consistant with the unit you use), then rate multiplied by time is the number of jobs. r*t=j, using j as a variable for how many jobs. Let's use those!

highlight%28%28r%2Br%2F2%29%282%261%2F3%29=1%29, we need to find r, the fill rate for the big pipe. Just algebra steps.

Remember, r is in units of jobs per hour. YOU want the reciprocal. When you find r, calculate its reciprocal. You want 1%2Fr, but easier first to find r.

post note: In fact even if you check the previous tutor's solution you will find your arithmetic mistake. A factor of 2 missing. My work gave me 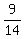14%2F9 jobs per hour which is 9%2F14 hours to fill the pool just through the big pipe. 39 minutes.