Question 711567: 4^log base 2 of 3
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Expressions of the form:
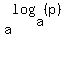
are very simple to simplify. Your expression

is not quite in that form because the base of the exponent, 4, is different from the base of the logarithm, 2. But here is where we can figure out a relatively simple solution. Aren't 4 and 2 powers of each other? ( and and  ). So we should be able to convert one base, the 4 or the 2, into the other. I'm going to change the base of 4 into a base of 2. Replacing the 4 with ). So we should be able to convert one base, the 4 or the 2, into the other. I'm going to change the base of 4 into a base of 2. Replacing the 4 with 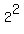 we get: we get:
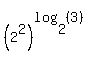
At this point we have a power of a power. The rule for the exponents for this is to multiply the exponents:
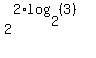
We have the bases matching. But we are still not quite in the desired form. The 2 in front of the log is the problem. But fortunately there is a property of logarithms,  , which allows us to move a coefficient in front of the log into the argument of the log as its exponent. Using this property we can move the 2 (which is in our way) into the argument as its exponent: , which allows us to move a coefficient in front of the log into the argument of the log as its exponent. Using this property we can move the 2 (which is in our way) into the argument as its exponent:
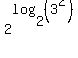
which simplifies to:

We now have the desired form. If you don't yet know how this simplifies, let's review what logarithms are. Logarithms in general are exponents. Base 2 logarithms are exponents one would put on a 2. More specifically,

is the exponent one would put on a 2 to get a result of 9. And look at where

is in our expression. It is the exponent on a 2! So our expression is "2 to the power that you would put on a 2 to get a result of 9". I hope it is clear that this means that
 must be a 9! must be a 9!
If this is not clear then either:- Memorize:
 ; or ; or - Learn to simplify it as follows. Let's say that:

Find the base a log of each side:

Use the property of logarithms mentioned earlier. This time, however, we are going to in the other direction: move the exponent of the argument out in front.

We should know that  so this simplifies to: so this simplifies to:

The equation now says that two base a logs are equal. If so then the arguments must be equal. So:

Since  and and  : :

|
|
|