Question 711452: (sqrt(x-2)) + 4 - (sqrt(x+2)) + (sqrt(3)) = 6
what is x? some of my friends who solved it say that there was no solution, but I want to know the work behind it, thanks!
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
A general procedure for solving equations like this is:- Isolate a square root (that has a variable in it).
- Square both sides of the equation.
- If there is still a square root (that has a variable in it), then repeat steps 1-3.
- At this point the equation should have no square roots (that have a variable in it). Use appropriate techniques to solve whatever kind of equation you now have.
- Check your solutions. This is not optional! Whenever you square both sides of an equation, like step 2, you must check for what are called extraneous solutions. Extraneous solutions are solutions that fit the squared equation but do not fit the original equation. They can occur even if no mistakes have been made. You must check for them and reject them if you find any.
Let's see this in action:
1. Isolate a square root.
The third square root does not have x in it so that is not a square root to isolate. we should isolate one of the other two square roots. I'm going to add the second square root to each side and subtract 6 from each side giving us:

At this point we might be able to see that there is no solution to this equation. Here's the logic:- Since the radicands (the expression within a radical is called a radicand) must not be negative we can tell that whatever x turns out to be x must be greater than or equal to 2.
- No matter what x turns out to be
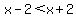 - Since
 , , 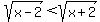 - Also
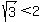 . This makes . This makes  (IOW: negative) (IOW: negative)
Putting this altogether:
- 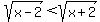
- 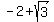 is negative is negative
- The equation says that a smaller square root plus a negative is equal to a larger square root.
- There are no solutions to the equation because it is impossible to take a smaller number 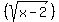 , add a negative and get a larger square root , add a negative and get a larger square root 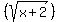 . (Note: An exception to this is when both square roots are between 0 and 1). Since . (Note: An exception to this is when both square roots are between 0 and 1). Since  , ,  . So we do not have this exception in this problem. So there are no solutions to this equation. . So we do not have this exception in this problem. So there are no solutions to this equation.
Note: I presented this logic because it is actually the "easy" way to solve this problem. But if you don't understand this or if you don't feel comfortable presenting this as your "work" or if your teacher would not accept such a logic-based solution, I will continue on with the procedure I outlined at the start...)
2. Square both sides.
Squaring the right side is as easy as it looks. But squaring the left side correctly will not be easy. It is not just squaring each term!! We have to multiply
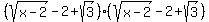
which is done by multiplying each of the three terms in the first factor by each of the three terms of the other factor and then adding like terms, if any. Before we start multiplying I'm going to change the subtraction into the equivalent addition because it is easier to avoid errors with additions:

Squaring both sides:

Simplifying...

(Note: I'm not multiplying 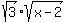 for a reason.) Adding like terms... for a reason.) Adding like terms...

3. We still have a square root with a variable in the radicand so it's back to step 1.
1. Isolate a square root (that has a variable in it).
Subtracting x and 5 from each side:

Adding 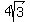 to each side: to each side:

Factoring out 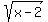 (which is why I didn't multiply (which is why I didn't multiply 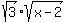 ): ):

Dividing by 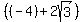 : :

(Note: Again we can save time and effort if we pay attention to what this equation says. The left side is a positive square root. The right side is a fraction with a positive numerator (since 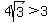 ) and a negative denominator (since ) and a negative denominator (since 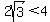 ) making the whole fraction negative (positive divided by negative is negative.) Since the positive left side cannot be equal to the negative right side, there are no solutions. But we will forge ahead with the procedure...) ) making the whole fraction negative (positive divided by negative is negative.) Since the positive left side cannot be equal to the negative right side, there are no solutions. But we will forge ahead with the procedure...)
2. Square both sides.
Squaring the isolated square root will be easy, as always. To square the right side I am going to take advantage of the  pattern to square the numerator and denominator: pattern to square the numerator and denominator:

Simplifying...



3. If there are square roots with a variable in it...
There are no more square roots with a variable. So on to step 4!
4. Solve the equation.
All we have to do is add 2:

5. Check your solution.
Use the original equation to check:

To make things a little easier I'm going to get a decimal approximation for  , use that to get a decimal approximation for x and then use that for the x in the check. (Note: Because of the use of approximations we may not get perfectly equal sides of the equation. If we get almost equal sides then we can hope that the answer checked. The only way to be sure is to avoid the use of approximations, i.e. check with , use that to get a decimal approximation for x and then use that for the x in the check. (Note: Because of the use of approximations we may not get perfectly equal sides of the equation. If we get almost equal sides then we can hope that the answer checked. The only way to be sure is to avoid the use of approximations, i.e. check with  , not some decimal.) , not some decimal.)
 , rounded to 3 places, is 1.732. Using this to get an approximation for x: , rounded to 3 places, is 1.732. Using this to get an approximation for x:






Now we can check:

Simplifying...



This is not close enough to equal to pass the check. (Again, if you want to be sure, don't use decimal approximations during the check!) So this solution must be rejected/discarded. And since we found no other possible solutions, there are no solutions to your original equation.
|
|
|