Question 711164: express log27 - log1/9 + (log51 - log17 / log81 - 2log3) + 4log1/3 + 3log3
In its simplest for. please note i don't know what ^ means when showing your working out
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 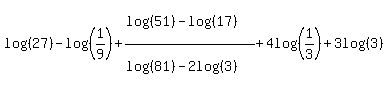
When I started thinking about how to simplify the expression one thing I noticed was that all the arguments (except 51 and 17) were powers of 3:





Then I noticed that the logs with arguments of 51 and 17 can be rewritten as a single log whose argument would also be a power of 3. All these powers of 3 will make simplifying the expression easier.
I'll start by rewriting the arguments (except 51 and 17) as powers of 3:

As we proceed we will be using several properties of logarithms:  
The first one we will use is #2. The numerator with log(51) and log(17) matches the right side of that property. So, according to that property, we can rewrite the two logs as a single log of 51/17:
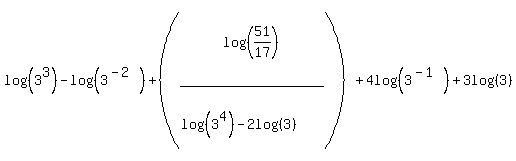
And since 51/17 = 3 we get:
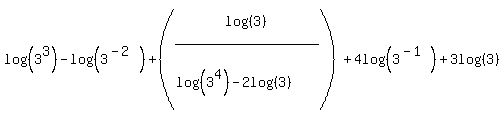
To use properties #1 and #2 the bases of the logs must be equal and the coefficients of the logs must be 1's. We will continue to use these properties to combine two logs into a single log. So we want all the logs to have coefficients of 1. Several of the logs do not have coefficients of 1, specifically the last log in the denominator and the last two logs terms. Fortunately property #3 gives us a way to handle these coefficients. The right side of Property #3 shows that the log has a coefficient of "n". The left side shows us that we can move the coefficient, n, into the argument as its exponent. Using this property on the three logs which do not have a coefficient of 1 we get:
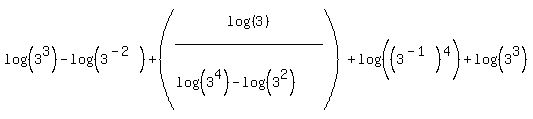
with the second-to-last log simplifying, according to the rules for exponents:
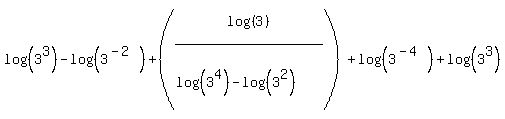
Now we can start using properties #1 and #2 to combine the remaining logs. Using property #2 on the first two logs:
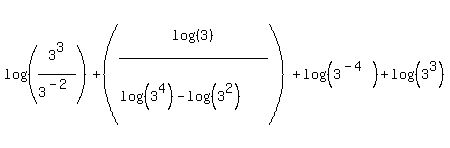
Again we can use the proper rule for exponents, subtract, to simplify the new argument:

Next we can use property #2 again to combine the two logs in the denominator:
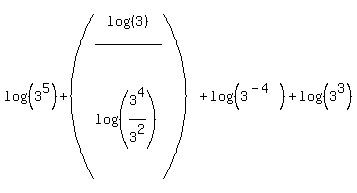
Again we subtract the exponents in the new argument:

Next we can use property #1 to combine the last two logs. (We use this property because its logs, like ours, have a "+" between them. All the previous pairs of logs had a "-" between them which is why we used property #2.)
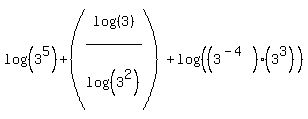
This time the rule for the exponents in our new argument is to add the exponents:
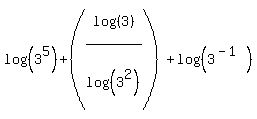
Next we can use property #1 again to combine the first and last logs. (This expression is all addition so we are allowed to change the order of the terms!)
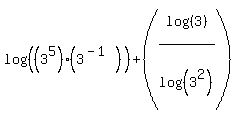
Again the rule for the exponents is to add:
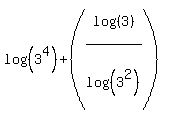
Next I will use property #3 again. This time I am going to use it in the reverse direction. I'm going to move the exponent on the argument of the log in the denominator back out in front. (By doing this I can get the two logs in the fraction to match (will allow us to cancel them.)
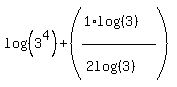
Now the log(3)'s in the fraction cancel out:

leaving:
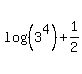
Last of all we can simplify our last remaining power of 3:
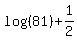
|
|
|