Question 711100: THREE INTEGERS ARE IN A GEOMETRIC SERIES, WHEN 12 IS ADDED TO THE SECOND TERM THE SERIES BECOMES AN ARITHMETIC SERIES AND WHEN 96 IS ALSO ADDED TO THE THIRD TERM THE SERIES CHANGES TO GEOMETRIC SERIES. WHAT ARE THE INTEGERS?
Answer by kevwill(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's call the three integers in the original series a, b, and c. Because this is a geometric series, we know that
 , so multiplying both sides by , so multiplying both sides by  gives gives


Adding 12 to the second number (b) gives an arithmetic series, so we know that
 , or , or

And finally, adding 96 to the third term of the new series gives us another geometric series, so we have
 , so multiplying both sides by , so multiplying both sides by 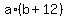 gives gives


and since  , we have , we have


And using 



From the equation above, c is only an integer when a is a factor if 36, so we can check the nine possibilities:
(1, -2, 4)
(2, 2, 2)
(3, 6, 12)
(4, 10, 25)
(6, 18, 54)
(9, 30, 100)
(12, 42, 147)
(18, 66, 242)
(36, 138, 529)
Of these 9 geometric series, only one generates an arithmetic series when 12 is added to the second term: (6, 18, 54)
Adding 12 to the second term gives the arithmetic series (6, 30, 54),
And adding 96 to the third term gives the geometric series (6, 30, 150).
|
|
|