Question 710746: im doing operations on expressions with exponents, can you help me solve some of my ?, like (2x^2 - x) + (x^2 + 3x -1) this is on of ?, i have a whole worksheet like this.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
I would "show my work" as just what's above or maybe as much as

I would think that should be enough showing work for someone working on polynomials, who is supposed to be able to be advanced enough to get to answers in one or two steps.
Show more or less work depending on what you think your teacher wants.
WORDY EXPLANATIONS:
Minus signs are a problem if you truly believe in subtraction.
By the time I was in college, I finally was told that subtraction and division do not really exist.
First I felt cheated, but afterwards I felt liberated.
Life is easier if you realize that "subtract 2" really means "add (-2)"
and  really means + really means +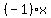 . .
Minus signs are not scary at all after that.
By the way, if you see
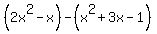
try to see it as

but just write it as
 for short, for short,
and keep saying "subtract" as needed,
because it is shorter than "add the opposite of".
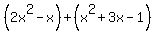 is a sum of two sums. is a sum of two sums.
The terms added in the first sum are the monomials  and and  . .
The terms added in the second sum are the monomials  , ,  and and  . .
Because of the associative and commutative properties of addition,
the terms in sums can be rearranged in different orders and associated in different groupings.
In sum,

because those parentheses, with the "(" right at the beginning, or immediately after a "+" sign are not really needed, and you can change the order and associations of the terms.
You can say that
 because of the distributive property, or because you are taking out because of the distributive property, or because you are taking out  as a common factor. as a common factor.
Or you could say that  is as obvious as "2 apples + 1 apple = 3 apples." is as obvious as "2 apples + 1 apple = 3 apples."
Similarly,

You can get as picky as you want, or use as few steps as absolutely needed to convince your teacher that you know what you are doing and "showed your work".
|
|
|