Question 7107: A boat took 1 hour and 5o minutes to go 55 miles downstream and 3 hours and 40 minutes to return. Find the rate of the current.
Thank you so much for helping me!!
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! AHA! A rate * time = distance type problem with twists!
DOWNSTREAM. We must agree that the boat has a rate when moving in still water. If downstream is with the current, then the boat actually traveled with its speed in still water plus the speed of the current. So far, then, we've got 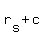 as the boat's "virtual" speed (AKA, the speed that it would be traveling if you're observing from the banks). as the boat's "virtual" speed (AKA, the speed that it would be traveling if you're observing from the banks).
The problem DID give us the fact that the boat took 1 hr 50 min to travel the 55 miles. Before doing any calculation here, we need to convert that 1 hr 50 min to fraction. That would be 1 5/6 hours, or put into an improper fraction, 11/6. (We'll use this because it's easier to calculate with).
Keep in mind that the rate that we'll get is the "virtual" speed because it includes the rate of the current! So, we've got rate = distance / time. (BTW, that's actually rate * time = distance rearranged algebraically). So  , and if you simplified, , and if you simplified,  . The "virtual" speed of the boat then would be 30 miles per hour. . The "virtual" speed of the boat then would be 30 miles per hour.
-------------------------------------------------------------------
UPSTREAM. We've got to agree that upstream travel is the boat's rate in still water against the current, so the upstream virtual rate is 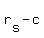 ***. They did tell us that the boat took 3 hours and 40 minutes to travel that same 55 miles. The 3h 40min in fraction would be 3 2/3, or the improper fraction 11/3. So how fast is that, then? Using the same distance = rate / time, we have ***. They did tell us that the boat took 3 hours and 40 minutes to travel that same 55 miles. The 3h 40min in fraction would be 3 2/3, or the improper fraction 11/3. So how fast is that, then? Using the same distance = rate / time, we have  which boils down to which boils down to  . From the observer at the bank, the boat's upstream "virtual" speed is 15 miles per hour. . From the observer at the bank, the boat's upstream "virtual" speed is 15 miles per hour.
--------------------------------------------------------------------
So now we've got the upstream and downstream rate equations:


It's now a system of linear equations. From this point on, I trust that you know how to solve this type of problem. Once you solve for 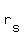 and and  , you'll see that the rate of the boat in still water is 22.5 miles per hour, and the rate of the current is 7.5 miles per hour. , you'll see that the rate of the boat in still water is 22.5 miles per hour, and the rate of the current is 7.5 miles per hour.
|
|
|