Question 710238: There are 100 seats and $100 to spend. $5.00 per seat for men, $2.00 per seat for women, $.10 per seat for children. How many of each to fill 100 seats?
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
m + w + c = 100
5m + 2w + .10c = 100
The number of children is a multiple of 10, so
it will come out to a whole number of dollars.
Let c = 10k
m + w + 10k = 100
5m + 2w + k = 100
Since these both = 100, set them equal:
m + w + 10k = 5m + 2w + k
9k - 4m = w
Substitute 9k - 4m for w in the first equation
m + w + 10k = 100
m + (9k - 4m) + 10k = 100
m + 9k - 4m + 10k = 100
-3m + 19k = 100
the smallest coefficient in absolute value is 3
So we write 19 and 100 in terms of their nearest
multiple of 3. So we write 19 as 18+1 and 100 as 99+1
-3m + (18+1)k = 99+1
-3m + 18k + k = 99 + 1
Divide through by 3
-m + 6k + 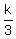 = 33 + = 33 +  Isolate the fractions:
Isolate the fractions:
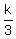 - -  = 33 + m - 6k
The right side is an integer, and so is the left side,
so set both sides = A, an integer: = 33 + m - 6k
The right side is an integer, and so is the left side,
so set both sides = A, an integer:
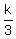 - -  = A; 33 + m - 6k = A
k - 1 = 3A
k = 3A+1
Substitute 3A+1 for k in 33 + m - 6k = A
33 + m - 6(3A+1) = A
33 + m - 18A - 6 = A
m = 19A - 27
Substitute 3A+1 for k and 19A-27 for m in 9k - 4m = w
9(3A+1) - 4(19A-27) = w
27A + 9 - 76A + 108 = w
117 - 49A = w
So we have m = 19A-27 men, 117-49A = w women, and c = 10k = 10(3A+1)
= 30A+10 children
We can't have a negative number of men, women or children
m ≧ 0
19A - 27 ≧ 0
19A ≧ 27
A ≧ = A; 33 + m - 6k = A
k - 1 = 3A
k = 3A+1
Substitute 3A+1 for k in 33 + m - 6k = A
33 + m - 6(3A+1) = A
33 + m - 18A - 6 = A
m = 19A - 27
Substitute 3A+1 for k and 19A-27 for m in 9k - 4m = w
9(3A+1) - 4(19A-27) = w
27A + 9 - 76A + 108 = w
117 - 49A = w
So we have m = 19A-27 men, 117-49A = w women, and c = 10k = 10(3A+1)
= 30A+10 children
We can't have a negative number of men, women or children
m ≧ 0
19A - 27 ≧ 0
19A ≧ 27
A ≧ 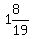 w ≧ 0
117 - 49A ≧ 0
-49A ≧ -117
A ≦
w ≧ 0
117 - 49A ≧ 0
-49A ≧ -117
A ≦ 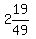 Thus
Thus 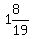 ≦ A ≦ ≦ A ≦ 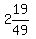 Therefore A = 2 since that is the only integer that
satisfies that inequality.
m = 19A - 27 = 19(2) - 27 = 38 - 27 = 11 men
w = 117 - 49A = 117 - 49(2) = 117 - 98 = 19 women
c = 30A + 10 = 30(2) + 10 = 60 + 10 = 70 children
Answer: 11 men, 19 women, and 70 children.
Edwin
Therefore A = 2 since that is the only integer that
satisfies that inequality.
m = 19A - 27 = 19(2) - 27 = 38 - 27 = 11 men
w = 117 - 49A = 117 - 49(2) = 117 - 98 = 19 women
c = 30A + 10 = 30(2) + 10 = 60 + 10 = 70 children
Answer: 11 men, 19 women, and 70 children.
Edwin
|
|
|