If you are in elementary school mathematics:
The sum of the digits of a certain two-digit number is 7.
So it's either 16, 25, 34, 43, 52, or 61
Reversing its digits increases the number by 9. what is the number?
Only 34 fits that bill, since 43 is 9 more than 34.
Answer for elementary school students: 34
-----------------
If you are in middle or high school algebra:
t = tens digit
u = units digit
10t+u = the number
10u+t = the number reversed
t+u = the sum of the digits.
The sum of the digits of a certain two-digit number is 7.
t+u = 7
Reversing its digits increases the number by 9. what is the number?
10u+t = (10t+u) + 9
The system to solve is
Simplify the second equation:
10u+t = (10t+u)+9
10u+t = 10t+u+9
9u-9t = 9
Divide through by 9
u-t = 1
Solve for u
u = 1+t
Substitute 1+t for u in
t+u = 7
t+(1+t) = 7
t+1+t = 7
1+2t = 7
Add -1 to both sides
2t = 6
Divide both sides by 2
= 
= 
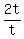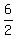
t = 3
Substitute 3 for t in
u = 1+t
u = 1+3
u = 4
Answer for middle school or high school students: 34.
Edwin
