|
Question 709367: What missing exponent would make this statement true?
81 5√27 = 3^?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I think the reason no tutor has responded to this earlier is that they do not understand what you posted. I'm making a guess that the left side is:
If I am right then please try to make your expressions clearer. Different kinds of roots can be difficult to post. For these either:- Use some English and parentheses to make it clear. For example, you could have used:
81 * (5th root(27)) - Or teach yourself the syntax for Algebra.com's expression-drawing software. Click on the "Show source" link above and you can see what I typed to get the root to display nicely. (It starts the three left braces, "{", then the special syntax, then it ends with three right braces, "}".
If I am wrong, then stop reading and re-post your problem in a clearer way.
Solving equations where the unknown/variable is in an exponent is easiest if it is possible to rewrite the equation so that both sides are power of the same number. So we will look to see if we can rewrite both sides of our equation this way. Looking at the numbers involved, 81, 27 and 3, it should not take a long time to figure out that all three of them are powers of 3. ( and  ) So we will be able to rewrite the equation in terms of powers of 3:
We can replace the radical with a fractional exponent:
Next we simplify. First the power of a power on the left side. The rule is to multiply the exponents:
Now we can multiply on the left side. The rule is to add the exponents:
We now have the equation in the desired form, two powers of 3 that are equal. The only way these powers of 3 can be equal is if the exponents are equal. So:
And we are finished.
P.S. In response to the question in your thank you note:
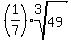
Both 1/7 and 49 are powers of 7:
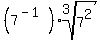
Changing the radical to a fractional exponent:
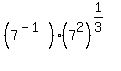
Using the rules for exponents to simplify:
|
|
|
| |
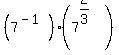
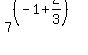
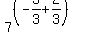
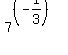
