SOLUTION: There exist pairs of integers, x and n, for which xn = (25)(4 to the 4th power)(8 to the 8/3 power )(16 to the 3/4 power). What is the greatest possible value of n among these pai

Algebra ->  Signed-numbers -> SOLUTION: There exist pairs of integers, x and n, for which xn = (25)(4 to the 4th power)(8 to the 8/3 power )(16 to the 3/4 power). What is the greatest possible value of n among these pai      Log On


   

Question 708707: There exist pairs of integers, x and n, for which xn = (25)(4 to the 4th power)(8 to the 8/3 power )(16 to the 3/4 power). What is the greatest
possible value of n among these pairs?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Of all the pairs (x,n) whose product is the same xn=N number, the greatest n will be paired with the least positive x.
Since N=1%2AN, the greatest integer that could be n is N
So we have to find N=%2825%29%2A%284%5E4%29%2A%288%5E%288%2F3%29%29%2A%2816%5E%283%2F4%29%29%5Eor N =(25)*(4^4)*(8^(8/3))*(16^(3/4))
Either way, that expression is hard to type.
Luckily, it can be simplified, because
16=2%5E4 --> 16^(3/4)=%28root%284%2C16%29%29%5E3=%28root%284%2C2%5E4%29%29%5E3=2%5E3
8=2%5E3 --> 8^(8/3)=%28root%283%2C8%29%29%5E8=%28root%283%2C2%5E3%29%29%5E8=2%5E8
and, while we are at it,
4=2%5E2 --> 4%5E4=%282%5E2%29%5E4=2%5E%282%2A4%29=2%5E8
So substituting all that, we get a large number that can be calculated with a calculator,
N=%2825%29%2A%282%5E8%29%2A%282%5E8%29%2A%282%5E3%29=highlight%2825%2A2%5E19%29 or with pencil and paper:


NOTE 1:
If it was specified that x, and n could not be 1,
then the least possible positive x would be 2,
and that would make 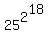25%5E2%5E18 the greatest possible n.

NOTE 2:
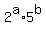
Since xn=25%2A2%5E19=2%5E19%2A5%5E2 the positive factors are all of the form 2%5Ea%2A5%5Eb
with a being any of the 20 integers from 0 to 19 including 0 and 19,
and b being 0, 1, or 2 (just 3 choices).
That makes the total number of positive factors 3%2A20=60.
That makes 60 (x,n) ordered pairs, or 30 {x,n} sets of factors (if order does not matter).
Considering the negative factors doubles the possibilities.