√3x+4 - √2x+4 = 2
Isolate either one of the radicals.
I'll isolate the first radical on the left side:
√3x+4 = 2 + √2x+4
Square both sides:
(√3x+4)² = (2 + √2x+4)²
3x+4 = (2 + √2x+4)(2 + √2x+4)
FOIL out the right side
3x+4 = 4 + 2√2x+4 + 2√2x+4 + 2x+4
3x+4 = 4 + 4√2x+4 + 2x+4
3x+4 = 8 + 4√2x+4 + 2x
Isolate the remaining radical term on the right:
x-4 = 4√2x+4
Square both sides:
(x-4)² = (4√2x+4)²
(x-4)(x-4) = 16(2x+4)
x²-8x+16 = 32x+64
x²-40x-48 = 0
That doesn't factor so we have to use the quadratic formula:
x =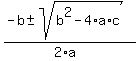 
x = 
x =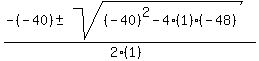 
x = 
x =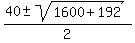 
x = 
x =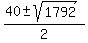 
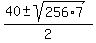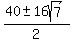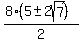x = 4(5 ± 2√7)
Using the +, x = 4(5 + 2√7), approximately 41.16601049
Using the -, x = 4(5 - 2√7), approximately -1.166010489
We must check for extraneous solutions:
√3x+4 - √2x+4 = 2
Checking 41.2 (rounded to tenths)
√3(41.2)+4 - √2(41.2)+4 = 2
√127.6 - √86.4 = 2
11.296 - 9.295 = 2
2.001 = 2
Not a perfect check, but close enough to believe it's
a solution, sibce we rounded off.
x = 4(5 + 2√7),
Checking -1.17 (rounded to hundredths)
√3(-1.17)+4 - √2(-1.17)+4 = 2
√2(41.2)+4 - √.49 = 2
.7 - 1.66 = 2
-.96 = 2
That's not close at all, so we believe it
is extraneous, and not a solution.
So there is just one solution: x = 4(5 + 2√7).
Edwin
(