Question 707114: what is the area of a triangle with side that are 9 units, 17 units and 10 units?
Found 2 solutions by lynnlo, KMST:
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I say that the area is  and here is the triangle: and here is the triangle:
 The small triangle, with sides measuring 6, 8, and 10 units is a right triangle, because the squares of the lengths of the shorter sides add up to the square of the length of the longer side: The small triangle, with sides measuring 6, 8, and 10 units is a right triangle, because the squares of the lengths of the shorter sides add up to the square of the length of the longer side:

A large triangle with sides measuring 15, 8, and 17 units is also a right triangle, because the squares of the lengths of the shorter sides add up to the square of the length of the longer side:

Our triangle with sides measuring 9, 10, and 17 units is the large right triangle minus the small right triangle, and its area is the difference between the areas of the two right triangles.
Area of the large right triangle= square units square units
Area of the small right triangle= square units square units
Area of the triangle in the problem= square units square units
When you only have the lengths of the sides, unless it is a right triangle, the problem is tricky. If you have not been taught enough, you need a combination of luck, ingenuity and triangle construction to figure out what I show in the drawing an explanation above. To construct a triangle with sides measuring 9, 10, and 17 cm, you would draw one of the sides to exact measure, and the use a compass to mark arcs centered at the ends of the first side, with radii matching the other two side lengths. Where the arcs meet is the third vertex of the triangle. Such a construction would help you figure out what I showed above.
If you have been taught about Heron's formula involving the semi-perimeter, you could use that.
If you were taught the law of cosines, you could use it to find the cosine (and then sine) of one angle, and then use the formula for area involving the lengths of two sides and the sine of the angle in between.
USING LAW OF COSINES:
 units = measure of shortest side units = measure of shortest side
 units = measure of medium length side units = measure of medium length side
 units = measure of longest side units = measure of longest side
 =measure of the largest angle, opposite longest. =measure of the largest angle, opposite longest.
The law of cosines says that
 so so  --> --> 
Solving for 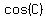 : :

 so so 
The area of a triangle can be calculated from the lengths of 2 sides, a and b, and the angle between them, C, as
 so so 
USING HERON'S FORMULA:
The semi-perimeter,  , is defined as half of the perimeter. , is defined as half of the perimeter.
If the side lengths are  , ,  , and , and  , then , then  , ,
and the area of the triangle is

 and and

|
|
|