|
Question 706615: Find the linear function satisfying the given conditions.
g(2) = 2 and the graph of g is perpendicular to the line 6x − 3y = 8.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  .....first write it in .....first write it in 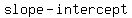 form form


 ......so, the slope is ......so, the slope is 
if  , the , the  and and  ; so, you have a point ( ; so, you have a point ( , , ) )
you also have a line  and the line you are looking for is perpendicular to this line and the line you are looking for is perpendicular to this line
now, we can find the linear function satisfying the given conditions
Remember, any two perpendicular lines are negative reciprocals of each other. So if you're given the slope of  , you can find the perpendicular slope by this formula: , you can find the perpendicular slope by this formula:
 where where 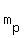 is the perpendicular slope; so, plug in the given slope to find the perpendicular slope is the perpendicular slope; so, plug in the given slope to find the perpendicular slope

now we know the slope of the unknown line (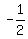 ) and a point ( ) and a point ( , , )=( )=( , , ); so, we can find the equation by plugging in this info into the point-slope formula ); so, we can find the equation by plugging in this info into the point-slope formula
 ....plug in ....plug in  , , , and , and 





or
 ...........this is a line that is perpendicular to the given graph and goes through ( ...........this is a line that is perpendicular to the given graph and goes through ( , , ) )
let's see it on a graph:

|
|
|
| |