Question 706542: Suppose You Have $77 For Tickets, and You want a total of 7 tickets. You want some weekday bleachers seats and some weekend lawn seats which are both $11. How many of each type of ticket can you buy? It also says To explain your reasoning. I have To write it in systems as well. Hope you can help.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A fifth grader could explain it, but not using systems of linear equations. That requires unnecessary complication.
 = number of weekday bleachers seats tickets = number of weekday bleachers seats tickets
 = number of weekend lawn seats tickets = number of weekend lawn seats tickets
Total number of ticket you are willing to purchase is
 because because
"You want a total of 7 tickets."
 weekday bleachers seats tickets will cost $ weekday bleachers seats tickets will cost $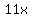
 weekend lawn seats tickets will cost $ weekend lawn seats tickets will cost $
because both cost $11 per ticket.
The total cost for
 weekday bleachers seats tickets plus weekday bleachers seats tickets plus
 weekend lawn seats tickets is weekend lawn seats tickets is
$
You can spend the total $ to buy to buy
 weekday bleachers seats tickets plus weekday bleachers seats tickets plus weekend lawn seats tickets, weekend lawn seats tickets,
spending  . .
To decide what to buy, you would solve the system

However, the system is what we call "dependent".
We also call it "undeterminate" because there is no unique solution.
The equations  and and  are equivalent and dependent, are equivalent and dependent,
because they are equivalent equations, with exactly the same solutions.
Here is what "equivalent equations" means:
 is what we get from is what we get from  by multiplying both sides of the equal sign times by multiplying both sides of the equal sign times  , ,
so all the solutions of  are solutions of are solutions of  . .
 is what we get from is what we get from  by dividing both sides of the equal sign by by dividing both sides of the equal sign by  , ,
so all the solutions of  are solutions of are solutions of   . .
In other words, if you have one equation, are you are given the other one,
you are not getting any new information.
All you know is that you can buy 7 tickets with the $77 you have.
(A fifth grader could tell you that).
You can buy all of your 7 tickets for weekday bleachers seats,
or you can buy all of your 7 tickets for weekend lawn seats,
or you could buy any combination of the two kinds of seats.
|
|
|