Question 706033: factor the trinomial 2x^2-5xy-3y^2
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The technique we will use to factor 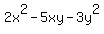 can be described as "un-FOIL-ing". FOIL is used to multiply expressions like (a+b)(c+d). Since factoring is, in effect, "un-multiplying" an expression we can use the reverse of FOIL to turn can be described as "un-FOIL-ing". FOIL is used to multiply expressions like (a+b)(c+d). Since factoring is, in effect, "un-multiplying" an expression we can use the reverse of FOIL to turn 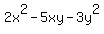 into an expression of the form (a+b)(c+d). into an expression of the form (a+b)(c+d).
If we have done enough FOIL-ing we know that when (a+b)(c+d) results in a trinomial, like 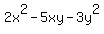 , then: , then:- The first term of the trinomial,
 , usually comes from the "F" part of FOIL (which would be a*c). For , usually comes from the "F" part of FOIL (which would be a*c). For  there is really only one possible "a" and "c": 2x and x. there is really only one possible "a" and "c": 2x and x. - The third term of the trinomial,
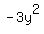 , usually comes from the "L" part of FOIL (which would be c*d). For , usually comes from the "L" part of FOIL (which would be c*d). For 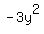 we could have two different c/d pairs: -3y and y or 3y and -y. we could have two different c/d pairs: -3y and y or 3y and -y. - The middle term of the trinomial, -5xy, usually comes from the sum of the "O" and "I" parts of FOIL (which would be a*d + b*c).
Now we just try the different possible values for a, b, c and d to see if any of them will create the proper middle term. (If none do then the trinomial will not factor.) As it turns out, there is a combination that works:
a = 2x, b = y, c = x and d = -3y
So 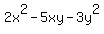 factors into: factors into:
(2x + y)(x + (-3y))
or, more simply:
(2x + y)(x - 3y)
To check this, just use FOIL!
|
|
|