|
Question 70524: Can someone please help me set-up and solve this problem
Solve and write in interval notation for the solution set
/x+2/ greater than or equal to 4
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
.
One method of solving this involves letting the entire quantity within the absolute
value signs first have a positive sign and then have a negative sign. Solve these two cases.
Perhaps it is best explained by using this problem as a typical example.
.
The quantity inside the absolute value signs is  . First write the inequality . First write the inequality
equation using +(x+2) for the left side. In this case the inequality becomes.
.

.
Solve this for x just as you would an ordinary equation ... by subtracting +2 from both
sides to get the answer as  . .
.
But that's only the first part of the solution. The second part says to give the entire
quantity inside the absolute value signs a negative sign and solve the inequality again.
.
So this time the inequality becomes:
.

.
You can remove the parentheses preceded by a negative sign by changing the sign of all the
terms inside the parentheses and then just erasing the parentheses. If you do this you
get:
.
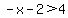
.
Begin the solution by adding 2 to both sides to eliminate the -2 on the left side. When
you do that, the inequality becomes:
.

.
Next comes a tricky part. You want to solve for positive x, so you are going to multiply both
sides by -1. However, if you multiply or divide both sides of an inequality by a negative
number you must reverse the direction of the inequality sign. No big deal, just something to
remember. So in this case after the multiplication and sign reversal the solution for x
becomes
.

.
In summary, the regions on the number line that satisfy the original inequality are any
value of x equal to or to the left of -6 and any value of x equal to or to the right of +2.
.
You can do a quick check by returning to the original problem and solve it for x = -7,
and x = +3. Or use any convenient value in the two regions ... for example x = - 10 and
x = + 10. You should see that the inequality is satisfied. Plus you can use any value
of x between -6 and +2 to prove to yourself that the original inequality is not satisfied by
values of x in that region. Usually x = 0 works well for this check because all the terms
containing x just disappear. It's usually a good idea to check the points you found on
the number line also. If you let x = -6 and then let x = +2, you should find that in
both cases the inequality of this problem is true only because of the equal sign associated
with the less than or greater than sign. Therefore, for this inequality x = -6
and x = +2
are included in the solution set.
.
In summary, solve two problems ... first use the entire quantity inside the absolute value
signs with a plus sign and solve the inequality for +x. ... next use the entire quantity inside
the absolute value signs with a negative sign and solve the inequality for +x. Don't forget
multiplication (or division) of both sides of the inequality by a negative number,
requires you to reverse the inequality sign. Finally use numbers in each of the regions that
you identify for the answer, and plug them into the original problem just to make sure
they work correctly. It also pays to check the end point numbers (in this problem they
were -6 and +2) to validate what region they fall into (are they part of the solution set
or are they not). [In this problem they were in the solution set because of the equal sign.]
.
Hope you find this method easy to remember and useful to you.
|
|
|
| |