Question 705215: I am not even sure what topic this problem falls under. It says, "Find the standard form of the equation of the circle for which the endpoints of a diameter are (0,0)and (4, -6).
Can you please help me with this?
Thanks!
Melissa
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If (0,0) and (4,-6) are endpoints of a diameter,
the midpoint of that diameter is the center of the circle.
Its coordinates are found by averaging the coordinates of those endpoints.
The x-coordinate is  . .
The y-coordinate is 
So, we have the center, C(2,-3).
A picture is work a thousand words:
 The radius, The radius,  , is the length of the segment form (0,0) to C(2,-3). , is the length of the segment form (0,0) to C(2,-3).
That segment is the hypotenuse of a right triangle (drawn in green).
We can calculate 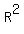 based on the Pythagorean theorem based on the Pythagorean theorem
 --> -->  --> --> 
Any point (x,y) in the circle is at the same distance  from the center, C. from the center, C.
As a consequence
 --> --> 
|
|
|