|
Question 704329: I am having a problem with fully understanding how to get an answer for these questions. I seriously do not understand how to get the domain, but I think I figured it out. If anyone can tell me where I went wrong it very simple terms that would be great. I apologize about there being more than 1 question.
1. Find the indicated function value.f(x) = x - 2, g(x) = x + 1Find (f + g)(-1)
Answer: -2 + 1 * -1 = 1
2. Find the domain of the function.f(x) = -3x + 2
Answer: (-∞, ∞)
3.For the pair of functions, determine the domain of f + g.f(x) = 2x + -9, g(x) = 4x + -3
Answer: (-∞, 0) or (0, ∞)
4. Find the requested value.f(x) = 2x2 - 1, g(x) = x + 1Find f(4) - g(4).
Answer: 34
5. For the pair of functions, determine the domain of f + g.f(x) = 4x + 3, g(x) = 3x + 8
Answer: (-∞, -4) or (-4, ∞)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. f(x) = x - 2, g(x) = x + 1
What they mean by (f + g)(-1) is the function made by adding functions f and g applied to x=-1.
You can calculate it as
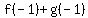 = [(-1)-2] + [(-1)+1] = = [(-1)-2] + [(-1)+1] =
or you can calculate 
and then substitute (-1) for x to get

It is not a product, and it is not ( -2 + 1) * (-1 )= 1
2. Find the domain of the function.f(x) = -3x + 2
Answer: (-∞, ∞)
You are correct. The domain of a function is the set of x values where it is defined.
Since there are no given restrictions on x,
and you can calculate it for any x,
the domain of f(x) = -3x + 2 is all real numbers.
(That is true of all polynomials).
3.For the pair of functions, determine the domain of f + g.f(x) = 2x + -9, g(x) = 4x + -3
Answer: (-∞, 0) or (0, ∞)
Why not (-∞, ∞)?
Do you think you could not calculate that function for x=0?
Denominators should not be zero, but I do not see any denominator in that function.
4. If  , and , and  , ,
 , and , and  , ,
Then  . .
5. f+g just indicates the function that is a sum of 2 functions.
f(x) = 4x + 3, and g(x) = 3x + 8 are polynomial functions.
They can be calculated for any real number x.
The sum can always be calculated, for any x.
The domain is all the real numbers
UNDERSTANDING DOMAIN:
The domain of a function is the set of x values where it is defined.
Examples:
If f(x) is defined as f(x) = 5 for all x>2,
then its domain is (2, ∞) because it is not defined for x=2, or for any x<2.
For a function without any explanation as to what x you are allowed to use,
you have to figure out if there is any value of x that will not work.
 does not exist (cannot be calculated) for x<0, does not exist (cannot be calculated) for x<0,
because there are no real square roots for negative numbers,
so its domain is [0, ∞)
 does not exist for x=3, because that would make the denominator zero, and we cannot divide by zero. does not exist for x=3, because that would make the denominator zero, and we cannot divide by zero.
We cannot calculate the function for x=3, so 3 is not part of the domain.
We can calculate  for all other numbers so its domain is for all other numbers so its domain is
(-∞, 3) or (3, ∞)
|
|
|
| |