Question 704266: if there is a triangle, the measurements of the three sides are 6, 8, and 10. what is the altitude of the triangle? it says to write a proportion and solve for x(the altitude). please help
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! An altitude of a triangle is a segment perpendicular to a side going from that side to the opposite vertex,
Because a triangle has 3 sides, there are 3 altitudes.
That particular triangle (as all triangles with side lengths in the ratio 3:4:5) is a right triangle.
Two of the altitudes are the legs of the right triangle (the shorter, perpendicular sides).
Each one is the altitude perpendicular to the other one.
We have to assume they want the other altitude, the one going from the side measuring 10 to the right angle.
 If you are supposed to realize that it is a right triangle,
you would conclude that the altitude divides the triangle into two similar triangles.
The pieces are similar to the original, larger right triangle,
because they have a pair of congruent right angles,
and a "pair" of congruent acute angles
(that are really the same angle shared by the original triangle and its smaller triangular piece).
In the original triangle, the angle at bottom right,
opposite the longer leg measuring 8,
is the larger of the acute angles,
and it is shared with the smaller triangle,
where it is opposite the small triangle's longer leg, which measures  .
Then, you could write proportions involving the length of corresponding sides in similar triangles.
For example, you could state that the ratio of long leg to hypotenuse is the same for the original triangle as for the smaller piece by writing the proportion
which can be solved by multiplying both sides of the equal sign times 6 to get
 -->  or 
If you are not supposed to realize that it is a right triangle,
you would not know that the triangles are similar, and would not be able to write the proportion as above. It may get complicated.
Of course, if you realized it was a right triangle, and you did not think about a proportion, you may calculate area of the triangle taking length of one leg as base, and the other as height as
area =
and knowing that also area =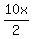 would figure out than  qnd  --> 
|
|
|
