Question 703928: 3^(12-x)=729 changes to Log3 729 = 12-x But I don't know where to go from here.
Found 2 solutions by josgarithmetic, josmiceli:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! The exponentiated result is the function's value. The logarithm is what exponent gave the function's value. The "logarithm" is the exponent. You are dealing just with an equivalent notation.
 is an equation in exponential form. The base is 3; the exponent is the logarithm and it is 12-x. The value 729 is the product or antilogarithm. So in "log" form, you write, "The logarithm, base 3":
 ,
"...of 729...",
 ,
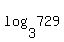... equals (12-x),
Continueing, you now have an equation with a term of x and no other variables. Subtract 12 from both sides, and multiply both sides by negative 1:
 , Solved.
(still some trouble learning the typesetting)
Answer by josmiceli(19441)  (Show Source):
|
|
|
