Question 703753: suppose that the end points of the longer leg of a 30-60-90 triangle are (-3,5) and (2-1). what is the length of the shorter leg?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The difference in x-coordinates between point (-3,5) and point(2,-1) is
 . .
The difference in y-coordinates between point (-3,5) and point(2,-1) is
 . .
The length of the longer leg connection those two points is
longer leg = 
That is not a friendly number.
Had the second point been (1,-2), the length would have been much friendlier:

In a 30-60-90 triangle the shorter leg is opposite the smaller,  angle, and the longer leg is adjacent to the angle, and the longer leg is adjacent to the  angle, so angle, so
 =(shorter leg)/(longer leg) --> shorter leg = =(shorter leg)/(longer leg) --> shorter leg =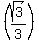 (longer leg) (longer leg)
So, if longer leg = 
Shorter leg =  = about = about 
The drawing below shows one of the four possible such triangles (with the vertices circled):
 All 4 have the red leg and a short leg on a perpendicular green line, but they could be flipped. All 4 have the red leg and a short leg on a perpendicular green line, but they could be flipped.
|
|
|